题目内容
7.已知数列{an}的前n项和为Sn,且2${S_n}={n^2}+n$.(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Sn.
分析 (1)利用递推关系即可得出;
(2)利用“裂项求和”、等差数列的前n项和公式即可得出.
解答 解:(1)由2${S_n}={n^2}+n$.
$n≥2时2{S_{n-1}}={(n-1)^2}+(n-1)$,
∴2an=2Sn-2Sn-1=2n,
∴an=n(n≥2),
又n=1时,a1=1适合上式.
∴an=n.
$(2)∵b{\;}_n=\frac{1}{{{a_n}{a_{n+1}}}}+2{a_n}-1=\frac{1}{n(n+1)}+2n-1=(\frac{1}{n}-\frac{1}{n+1})+(2n-1)$,
∴${S_n}=[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{n}-\frac{1}{n+1})]+(1+3+…+2n-1)$
=$1-\frac{1}{n+1}+{n^2}={n^2}+1-\frac{1}{n+1}$.
点评 本题考查了递推关系、“裂项求和”、等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
15.θ在第四象限,则 $\frac{θ}{2}$ 所在的象限为( )
| A. | 第一象限或第三象限 | B. | 第二象限或第四象限 | ||
| C. | 第三象限 | D. | 第四象限 |
2.函数y=$\frac{1}{x}$在x=1到x=2之间的平均变化率为( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | -2 | D. | 2 |
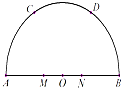 如图AB是半圆O的直径,C,D是弧$\widehat{AB}$的三等分点,M,N是线段AB的三等分点,若OA=6,则$\overrightarrow{MC}•\overrightarrow{ND}$=( )
如图AB是半圆O的直径,C,D是弧$\widehat{AB}$的三等分点,M,N是线段AB的三等分点,若OA=6,则$\overrightarrow{MC}•\overrightarrow{ND}$=( )