题目内容
 如图,一个圆心角为270°,半径为2m的扇形工件,未搬动前如图所示,A,B两点触地放置,搬动时,先将扇形以B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A,B两点再次触地时停止,则圆心O所经过的路线长是
如图,一个圆心角为270°,半径为2m的扇形工件,未搬动前如图所示,A,B两点触地放置,搬动时,先将扇形以B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A,B两点再次触地时停止,则圆心O所经过的路线长是考点:进行简单的合情推理
专题:综合题,三角函数的求值
分析:O经过的路线是两个半径是2,圆心角的45°的弧,平移的距离是半径长是2,圆心角是270°的弧长,二者的和就是所求的路线长.
解答:
解:∠AOB=360°-270°=90°,则∠ABO=45°,
∴∠OBC=45°,
O旋转的长度是:2×
=π;
O移动的距离是:
=3π,
∴圆心O所经过的路线长是:π+3π=4π,
故答案是:4π.
∴∠OBC=45°,
O旋转的长度是:2×
| 45π×2 |
| 180 |
O移动的距离是:
| 270π×2 |
| 180 |
∴圆心O所经过的路线长是:π+3π=4π,
故答案是:4π.
点评:本题考查了弧长的计算公式,正确理解O经过的路线是关键,难度较大,.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
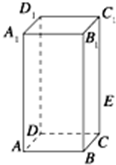 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.试建立适当的坐标系,写出点B、C、E、A1的坐标.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.试建立适当的坐标系,写出点B、C、E、A1的坐标.