题目内容
定义在R上的函数f(x)满足(x+2)f ′(x)<0(其中f ′(x)是函数f(x)的导数),又a=f(log 3),b=f[(
3),b=f[(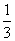 )0.1],c=f(ln3),则a,b,c的大小关系为______.(从大到小排列)
)0.1],c=f(ln3),则a,b,c的大小关系为______.(从大到小排列)
a>b>c
[解析] 因为-2=log 4<log
4<log 3<log
3<log 1=0,0<(
1=0,0<(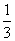 )0.1<(
)0.1<(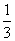 )0=1,ln3>ln e=1,因而-2<log
)0=1,ln3>ln e=1,因而-2<log 3<(
3<(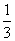 )0.1<ln3.由(x+2)f ′(x)<0知,当x>-2时,f ′(x)<0,所以f(x)在(-2,+∞)上是减函数,从而f(log
)0.1<ln3.由(x+2)f ′(x)<0知,当x>-2时,f ′(x)<0,所以f(x)在(-2,+∞)上是减函数,从而f(log 3)>f[(
3)>f[(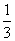 )0.1]>f(ln3),即a>b>c.
)0.1]>f(ln3),即a>b>c.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 上,α为曲线在P处的切线的倾斜角,则α的取值范围为( )
上,α为曲线在P处的切线的倾斜角,则α的取值范围为( )
 (k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
(k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.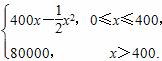 则总利润最大时,每年生产的产品产量是( )
则总利润最大时,每年生产的产品产量是( )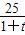 (t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )
(t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )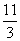
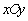 中,圆
中,圆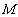 的方程为
的方程为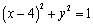 .以原点
.以原点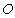 为极点,以
为极点,以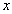 轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线
轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线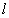 的极坐标方程为
的极坐标方程为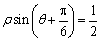 .
.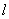 的距离的最小值.
的距离的最小值.