题目内容
12．设等差数列{an}的前n项和为Sn，等差数列{bn}的前n项和为Tn，若$\frac{{S}_{n}}{{T}_{n}}$=$\frac{7n+3}{n+3}$，求$\frac{{a}_{n}}{{b}_{n}}$．分析 由等差数列的通项公式和前n项和公式推导出$\frac{{a}_{n}}{{b}_{n}}$=$\frac{{S}_{2n-1}}{{T}_{2n-1}}$，由此能求出结果．
解答 解：∵等差数列{an}的前n项和为Sn，等差数列{bn}的前n项和为Tn，$\frac{{S}_{n}}{{T}_{n}}$=$\frac{7n+3}{n+3}$，
∴$\frac{{a}_{n}}{{b}_{n}}$=$\frac{2{a}_{n}}{2{b}_{n}}$=$\frac{{a}_{1}+{a}_{2n-1}}{{b}_{1}+{b}_{2n-1}}$=$\frac{\frac{2n-1}{2}（{a}_{1}+{a}_{2n-1}）}{\frac{2n-1}{2}（{b}_{1}+{b}_{2n-1}）}$
=$\frac{{S}_{2n-1}}{{T}_{2n-1}}$=$\frac{7（2n-1）+3}{（2n-1）+3}$=$\frac{7n-2}{n+1}$．
点评 本题考查两个等差数列中某一项比值的求法，是中档题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
2．设点P是△ABC所在平面内的一点，$\overrightarrow{PA}$+2$\overrightarrow{PB}$+3$\overrightarrow{PC}$=4$\overrightarrow{AB}$，且△ABC的面积为S，则下列判断正确的是（ ）
| A． | 点P在△ABC外，且△APC的面积为$\frac{1}{3}$S | B． | 点P在△ABC外，且△APC的面积为$\frac{1}{2}$S | ||
| C． | 点P在△ABC内，且△APC的面积为$\frac{1}{3}$S | D． | 点P在△ABC内，且△APC的面积为$\frac{1}{2}$S |
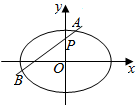如图，椭圆E：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率是$\frac{\sqrt{3}}{2}$，过点P（0，1）的动直线l与椭圆相交于A、B两点，当直线l平行于x轴时，直线l被椭圆E截得的线段长为4．
1．若复数z满足：iz=i+z，则z=（ ）
| A． | 1+i | B． | 1-i | C． | $\frac{1+i}{2}$ | D． | $\frac{1-i}{2}$ |