题目内容
如图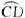
图
证明:连结BD、CD,
∵四边形ABCD是圆内接四边形,
∴∠1=∠BCD.∵![]() =
=![]() ,∴∠DBC=∠2.又∠1=∠2,∴∠DBC=∠BCD.
,∴∠DBC=∠2.又∠1=∠2,∴∠DBC=∠BCD.
∴BD=CD,即△BDC是等腰三角形.
而F是底边BC中点,
∴DF⊥BC.

练习册系列答案
相关题目
题目内容
如图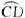
图
证明:连结BD、CD,
∵四边形ABCD是圆内接四边形,
∴∠1=∠BCD.∵![]() =
=![]() ,∴∠DBC=∠2.又∠1=∠2,∴∠DBC=∠BCD.
,∴∠DBC=∠2.又∠1=∠2,∴∠DBC=∠BCD.
∴BD=CD,即△BDC是等腰三角形.
而F是底边BC中点,
∴DF⊥BC.
