题目内容
如图2-3-19,已知AB是圆O的直径,C是圆周上不同于A、B的点,PA垂直于圆O所在平面,AE⊥PB于E,AF⊥PF于F.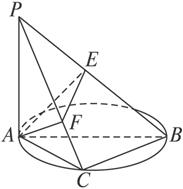
图2-3-19
求证:平面AEF⊥平面PBC.
证明:∵AB为⊙O的直径,
∴BC⊥AC.
∵PA⊥面ABC,BC
面ABC,∴PA⊥BC.
∵PA∩AC=A,
∴BC⊥平面PAC.
而AF
平面PAC,∴BC⊥AF.
又AF⊥PC,BC∩PC=C,
∴AF⊥平面PBC.
∵PB
平面PBC,∴AF⊥PB.
又∵AE⊥PB,AE∩AF=A,
∴PB⊥平面AEF.
∵PB
平面PBC,∴平面AEF⊥平面PBC.
练习册系列答案
相关题目
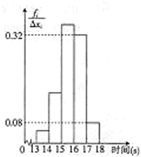（2012•安徽模拟）为了了解某年级1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）；…；第五组[17，18]．按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3：8：19，且第二组的频数为8．
