题目内容
15．已知变量x，y满足不等式组$\left\{\begin{array}{l}{3x+y-15≤0}\\{x-3y-5≤0}\\{x≥a}\end{array}\right.$使得y≥3x恒成立的实数a的最小值为（ ）| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 画出约束条件的可行域，利用指数式恒成立，转化求解a的最小值即可．
解答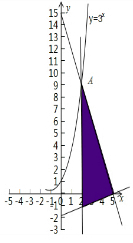 
解：变量x，y满足不等式组$\left\{\begin{array}{l}{3x+y-15≤0}\\{x-3y-5≤0}\\{x≥a}\end{array}\right.$的可行域如图：
变量x，y满足不等式组$\left\{\begin{array}{l}{3x+y-15≤0}\\{x-3y-5≤0}\\{x≥a}\end{array}\right.$使得y≤3x恒成立，
可知可行域的A是最优解，此时3x取得最大值，由$\left\{\begin{array}{l}{x=a}\\{3x+y-15=0}\end{array}\right.$，
可得A（a，15-3a），
15-3a≤3a，此时a≥2，
变量x，y满足不等式组$\left\{\begin{array}{l}{3x+y-15≤0}\\{x-3y-5≤0}\\{x≥a}\end{array}\right.$使得y≥3x恒成立的实数a的最小值为2．
故选：C．
点评 本题考查线性规划的简单应用，函数的最值以及恒成立条件的转化，考查计算能力．
练习册系列答案
相关题目
5．有四人在海边沙滩上发现10颗精致的珍珠，四人约定分配方案：四人先抽签排序①②③④，再由①号提出分配方案，四人表决，至少要有半数的赞成票才算通过，若通过就按此方案分配，否则提出方案的①号淘汰，不再参与分配，接下来由②号提出分配方案，三人表决…，依此类推．假设：1．四人都守信用，愿赌服输；2．提出分配方案的人一定会赞成自己的方案；3．四人都会最大限度争取个人利益．易知若①②都淘汰，则③号的最佳分配方案（能通过且对提出方案者最有利）是（10，0）（表示③、④号分配珍珠数分别是10和0）．问①号的最佳分配方案是（ ）
| A． | （4，2，2，2） | B． | （9，0，1，0） | C． | （8，0，1，1） | D． | （7，0，1，2） |
3．某学校想要调查全校同学是否知道迄今为止获得过诺贝尔物理奖的6位华人的姓名，为此出了一份考卷，该卷共有6个单选题，每题答对得20分，答错、不答得零分，满分120分，阅卷完毕后，校方公布每题答对率如下：
则此次调查全体同学的平均分数是52分．
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 |
| 答对率 | 70% | 60% | 50% | 40% | 30% | 10% |
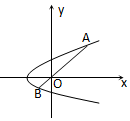在抛物线y2=4a（x+a）（a＞0），设有过原点O作一直线分别交抛物线于A、B两点，如图所示，试求|OA|•|OB|的最小值．