题目内容
若定义在R上的函数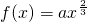 (a为常数)满足f(-2)>f(1),则f(x)的最小值是________.
(a为常数)满足f(-2)>f(1),则f(x)的最小值是________.
0
分析:根据f(-2)>f(1)得到a>0,从而有定义在R上的函数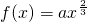 (a为常数)是偶函数,再结合此偶函数f(x)在[0,+∞)上是单调增函数,在(-∞,0]上是单调减函数,从而得出f(x)的最小值.
(a为常数)是偶函数,再结合此偶函数f(x)在[0,+∞)上是单调增函数,在(-∞,0]上是单调减函数,从而得出f(x)的最小值.
解答:由f(-2)>f(1)得,
 ,
,
解得:a>0,
又定义在R上的函数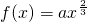 (a为常数)是偶函数,
(a为常数)是偶函数,
且偶函数f(x)在[0,+∞)上是单调增函数,在(-∞,0]上是单调减函数,
所以f(x)min=f(0)=0;
故答案为:0.
点评:本题主要考查幂函数的性质、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,属于基础题.
分析:根据f(-2)>f(1)得到a>0,从而有定义在R上的函数
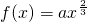 (a为常数)是偶函数,再结合此偶函数f(x)在[0,+∞)上是单调增函数,在(-∞,0]上是单调减函数,从而得出f(x)的最小值.
(a为常数)是偶函数,再结合此偶函数f(x)在[0,+∞)上是单调增函数,在(-∞,0]上是单调减函数,从而得出f(x)的最小值.解答:由f(-2)>f(1)得,
 ,
,解得:a>0,
又定义在R上的函数
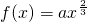 (a为常数)是偶函数,
(a为常数)是偶函数,且偶函数f(x)在[0,+∞)上是单调增函数,在(-∞,0]上是单调减函数,
所以f(x)min=f(0)=0;
故答案为:0.
点评:本题主要考查幂函数的性质、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
对于函数f(x),若?a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三边长,则称f(x)为“可构造三角形函数”.以下说法正确的是( )
| A、f(x)=1(x∈R)不是“可构造三角形函数” | ||
| B、“可构造三角形函数”一定是单调函数 | ||
C、f(x)=
| ||
D、若定义在R上的函数f(x)的值域是[
|