题目内容
函数f(x)=x
-(
)x的零点个数为( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、0 | B、1 | C、2 | D、3 |
考点:函数零点的判定定理
专题:数形结合
分析:令f(x)=0,即x
=(
)x,画出函数y=x
与y=(
)x的图象,观察两函数图象的交点个数即可.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:
解:令f(x)=0,即x
=(
)x,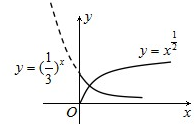
则函数f(x)=x
-(
)x的零点个数等价于函数y=x
与y=(
)x图象的交点个数.
在同一坐标系中作出函数y=x
与y=(
)x图象,如右图所示.
由图知,两函数图象只有一个交点,所以函数的零点个数为1.
故答案为:B.
| 1 |
| 2 |
| 1 |
| 3 |
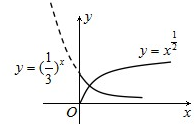
则函数f(x)=x
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
在同一坐标系中作出函数y=x
| 1 |
| 2 |
| 1 |
| 3 |
由图知,两函数图象只有一个交点,所以函数的零点个数为1.
故答案为:B.
点评:对于由两个函数构成的函数的零点个数问题,求解的一般步骤是:先转化为方程的实根问题,整理成两边各一个函数,再作出两函数的图象,从而将零点问题转化为两函数图象的交点个数问题.体现了函数与方程思想、转化与化归思想、数形结合思想等.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
设集合M={0,1,2},N={x|x2≤x},则M∩N=( )
| A、{0} | B、{1} |
| C、{0,1} | D、{0,1,2} |
有7名大学生志愿者,每人至少会英语和日语中的一种语言,其中会英语的有5人,会日语的有4人,现从中选派2人去担任日语翻译,再选派2人担任英语翻译,则选派方法的种数为( )
| A、37 | B、35 | C、31 | D、28 |
已知a=log23,b=log46,c=log
,则a,b,c的大小关系为( )
| 1 |
| 2 |
| 1 |
| 7 |
| A、a>b>c |
| B、b>a>c |
| C、c>b>a |
| D、c>a>b |
y=cosx,x∈[0,
]的图象与直线y=
的交点的个数为( )
| 5π |
| 2 |
| 1 |
| 3 |
| A、0 | B、1 | C、2 | D、3 |
函数f(x)=x3-2的零点所在的区间是( )
| A、(-2,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
直线l1:(
-1)x+y-2=0与直线l2:x+(
+1)y-3=0的位置关系是( )
| 2 |
| 2 |
| A、平行 | B、相交 | C、垂直 | D、重合 |
在[0,2π]内,不等式sinx<-
的解集是( )
| ||
| 2 |
| A、(0,π) | ||||
B、(
| ||||
C、(
| ||||
D、(
|