题目内容
已知P(-4,-4),Q是椭圆x2+2y2=16上的动点,M是线段PQ上的点,且满足PM=
MQ,则动点M的轨迹方程是( )
| 1 |
| 3 |
| A、(x-3)2+2(y-3)2=1 |
| B、(x+3)2+2(y+3)2=1 |
| C、(x+1)2+2(y+1)2=9 |
| D、(x-1)2+2(y-1)2=9 |
分析:设动点M(x,y),Q(m,n),则有
+
=1 ①,由
=
,得到m=4(x+3),n=4(y+3),代入①化简可得结果.
| m2 |
| 16 |
| n2 |
| 8 |
| PM |
| 1 |
| 3 |
| MQ |
解答:解:椭圆x2+2y2=16 即
+
=1,设动点M(x,y),Q(m,n),则有
+
=1 ①.
∵
=
,∴
,∴m=4(x+3),n=4(y+3),代入①化简可得
(x+3)2+2(y+3)2=1,
故选 B.
| x2 |
| 16 |
| y2 |
| 8 |
| m2 |
| 16 |
| n2 |
| 8 |
∵
| PM |
| 1 |
| 3 |
| MQ |
|
(x+3)2+2(y+3)2=1,
故选 B.
点评:本题考查用代入法求点的轨迹方程,得到
,是解题的关键.
|

练习册系列答案
相关题目
 (a>b>0)上一点,F1,F2是椭圆的左、右焦点,若使△PF1F2为直角三角形的点P有且只有4个,则椭圆离心率的取值范围是( )
(a>b>0)上一点,F1,F2是椭圆的左、右焦点,若使△PF1F2为直角三角形的点P有且只有4个,则椭圆离心率的取值范围是( )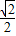 )
) ,1)
,1) )
) ,+∞)
,+∞)