题目内容
已知P为椭圆 (a>b>0)上一点,F1,F2是椭圆的左、右焦点,若使△PF1F2为直角三角形的点P有且只有4个,则椭圆离心率的取值范围是( )
(a>b>0)上一点,F1,F2是椭圆的左、右焦点,若使△PF1F2为直角三角形的点P有且只有4个,则椭圆离心率的取值范围是( )A.(0,
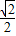 )
)B.(
 ,1)
,1)C.(1,
 )
)D.(
 ,+∞)
,+∞)
【答案】分析:利用椭圆和离心率的计算公式即可得出.
解答:解:①当PF1⊥x轴时,由两个点P满足△PF1F2为直角三角形;同理当PF2⊥x轴时,由两个点P满足△PF1F2为直角三角形.
∵使△PF1F2为直角三角形的点P有且只有4个,
∴以原点为圆心,c为半径的圆与椭圆无交点,∴c<b,
∴c2<b2=a2-c2,∴ ,又e>0,解得
,又e>0,解得 .
.
故选A.
点评:熟练掌握椭圆和离心率的计算公式是解题的关键.
解答:解:①当PF1⊥x轴时,由两个点P满足△PF1F2为直角三角形;同理当PF2⊥x轴时,由两个点P满足△PF1F2为直角三角形.
∵使△PF1F2为直角三角形的点P有且只有4个,
∴以原点为圆心,c为半径的圆与椭圆无交点,∴c<b,
∴c2<b2=a2-c2,∴
 ,又e>0,解得
,又e>0,解得 .
.故选A.
点评:熟练掌握椭圆和离心率的计算公式是解题的关键.

练习册系列答案
相关题目
 (a>b>0)上任意一点,P与两焦点连线互相垂直,且P到两准线距离分别为6、12,则椭圆方程为( )。
(a>b>0)上任意一点,P与两焦点连线互相垂直,且P到两准线距离分别为6、12,则椭圆方程为( )。