题目内容
4．设函数f（x）为奇函数，g（x）=f（x）+2，g（-2）=3，则f（2）=-1．分析 根据函数的奇偶性得到f（-2）=-f（2），结合g（-2）=f（-2）+2=3，求出f（2）的值即可．
解答 解：∵f（-x）=-f（x），∴f（-2）=-f（2），
∴g（-2）=f（-2）+2=3，
∴f（-2）=1=-f（2），
∴f（2）=-1，
故答案为：-1．
点评 本题考查了函数的奇偶性问题，考查求函数值问题，是一道基础题．
练习册系列答案
相关题目
19．与-$\frac{π}{2}$终边相同的角是（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{3π}{2}$ | D． | 2π |
9．已知集合A={x|2x＜2}，B={y|y=$\sqrt{x}$}，则A∩B=（ ）
| A． | [0，1） | B． | （0，2） | C． | （1，+∞） | D． | [0，+∞） |
1．
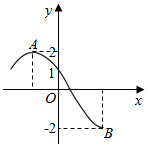如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤$\frac{π}{2}$）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）
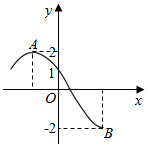如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤$\frac{π}{2}$）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）| A． | -1 | B． | -$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | 1 |