题目内容
(14)已知函数![]()
(Ⅰ)求函数![]() 的极值;
的极值;
(Ⅱ)对于曲线上的不同两点![]() ,如果存在曲线上的点
,如果存在曲线上的点![]() ,且
,且![]() ,使得曲线在点
,使得曲线在点![]() 处的切线
处的切线![]() ,则称
,则称![]() 为弦
为弦![]() 的伴随切线.当
的伴随切线.当![]() 时,已知两点
时,已知两点![]() ,试求弦
,试求弦![]() 的伴随切线
的伴随切线![]() 的方程;O%M
的方程;O%M
(Ⅲ)设![]() ,若在
,若在![]() 上至少存在一个
上至少存在一个![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围。O%
的取值范围。O%
解:(I)![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 内是减函数,
内是减函数,
![]() 函数
函数![]() 没有极值.
没有极值.
当![]() 时,令
时,令![]() 得
得![]()
![]()
当![]() 变化时,
变化时,![]() 与
与![]() 变化情况如下表:
变化情况如下表:
| |
|
|
|
|
| - | 0 | + |
|
| 单调递减 | 极小值 | 单调递增 |
![]() 当
当![]() 时,
时,![]() 取得极小值
取得极小值![]() .
.
综上,当![]() 时,
时,![]() 没有极值;
没有极值;
当![]() 时,
时,![]() 的极小值为
的极小值为![]() ,没有极小值
,没有极小值![]()
(Ⅱ)当![]() 时,设切点
时,设切点![]() ,则切线
,则切线![]() 的斜率为
的斜率为![]() .
.
弦AB的斜率为![]() .
.
由已知得,![]() ,则
,则![]() =
=![]() ,解得
,解得![]() ,
,
所以,弦![]() 的伴随切线
的伴随切线![]() 的方程为:
的方程为:![]() .
.
(Ⅲ)
本命题等价于![]() 在
在![]() 上有解,
上有解,
设![]()
![]() ,
,
![]()
![]() ,
,
所以![]() 为增函数,
为增函数,![]() .
.
依题意需![]() ,解得
,解得![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
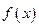 在定义域
在定义域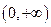 上为增函数,且满足
上为增函数,且满足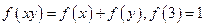
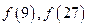 的值 (2)解不等式
的值 (2)解不等式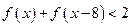
 在
在 处取得极值。
处取得极值。 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
; 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。 .
. 的最大值及取得最大值时的
的最大值及取得最大值时的 集合;
集合; 的角
的角 的对边分别为
的对边分别为 ,且
,且 .求
.求 的取值范围.
的取值范围.