题目内容
2.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F(c,0),圆F:(x-c)2+y2=c2,直线l与双曲线C的一条渐近线垂直且在x轴上的截距为$\frac{2}{3}$a.若圆F被直线l所截得的弦长为$\frac{4\sqrt{2}}{3}$c,则双曲线的离心率为( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | 3 |
分析 由题意,设直线方程为y=-$\frac{a}{b}$(x-$\frac{2}{3}$a),即$\frac{a}{b}$x+y-$\frac{2{a}^{2}}{3b}$=0,利用圆F被直线l所截得的弦长为$\frac{4\sqrt{2}}{3}$c,可得圆心到直线的距离d=$\frac{|\frac{ac}{b}-\frac{2{a}^{2}}{3b}|}{\sqrt{\frac{{a}^{2}}{{b}^{2}}+1}}$=$\sqrt{{c}^{2}-(\frac{2\sqrt{2}}{3}c)^{2}}$,即可求出双曲线的离心率.
解答 解:由题意,设直线方程为y=-$\frac{a}{b}$(x-$\frac{2}{3}$a),即$\frac{a}{b}$x+y-$\frac{2{a}^{2}}{3b}$=0,
∵圆F被直线l所截得的弦长为$\frac{4\sqrt{2}}{3}$c,
∴圆心到直线的距离d=$\frac{|\frac{ac}{b}-\frac{2{a}^{2}}{3b}|}{\sqrt{\frac{{a}^{2}}{{b}^{2}}+1}}$=$\sqrt{{c}^{2}-(\frac{2\sqrt{2}}{3}c)^{2}}$,
∴e2-3e+2=0,
∵e>1,
∴e=2,
故选C.
点评 本题考查双曲线的离心率,考查直线与圆的位置关系的运用,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
13.已知关于x的方程为x2+x+n2=0,若n∈[-1,1],则方程有实数根的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
10.设全集U=R,$A=\left\{{x|\frac{x-3}{x-1}>0}\right\}$,B={x|x<2},则(∁UA)∩B=( )
| A. | {x|1≤x<2} | B. | {x|1<x<2} | C. | {x|x<2} | D. | {x|x≥1} |
14.已知i是虚数单位,复数$z=i+\frac{2}{1-i}$,则复数$\overline z$的虚部是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}$ | D. | -2 |
12.已知集合A={x||x|≤2},B={x|x2-2x-3≤0},则A∩B=( )
| A. | [-1,2] | B. | [-2,3] | C. | [-2,1] | D. | [1,2] |
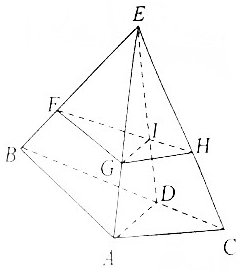 在三棱锥E-ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,点D在线段BC上,且BD=2CD,ED⊥平面ABC,F,G,H是EB,EA,EC上的点,FH与ED交于点I.
在三棱锥E-ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,点D在线段BC上,且BD=2CD,ED⊥平面ABC,F,G,H是EB,EA,EC上的点,FH与ED交于点I.