题目内容
数列{an}的通项 ,其前n项和为Sn,则S24的值为( )
,其前n项和为Sn,则S24的值为( )A.470
B.360
C.304
D.169
【答案】分析:利用二倍角的公式化简可得一个三角函数,根据周期公式求出周期为3,可化简S24,求出值即可;
解答:解:令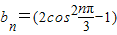 ,
,
可得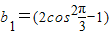 =2×
=2× -1=-
-1=- ,
,
b2=2× -1=-
-1=- ,
,
b3=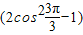 =1,
=1,
b4=- ,b5=-
,b5=- ,b6=1
,b6=1
可以推出周期为3,
∴S24=b1+b2+b3+b4+…+b24=- (12+22+42+52+72+…+232)+(32+62+92+…+242)
(12+22+42+52+72+…+232)+(32+62+92+…+242)
=- (12+22+32+…+242)+
(12+22+32+…+242)+ (32+62+92+…+242)
(32+62+92+…+242)
=- ×
×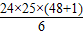 +
+ ×1835
×1835
=-2450+2754
=304;
故选C;
点评:考查学生会求数列的和,掌握三角函数周期的计算方法,计算量比较大,考查学生的计算能力,是一道中档题;
解答:解:令
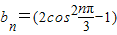 ,
,可得
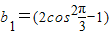 =2×
=2× -1=-
-1=- ,
,b2=2×
 -1=-
-1=- ,
,b3=
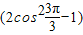 =1,
=1,b4=-
 ,b5=-
,b5=- ,b6=1
,b6=1可以推出周期为3,
∴S24=b1+b2+b3+b4+…+b24=-
 (12+22+42+52+72+…+232)+(32+62+92+…+242)
(12+22+42+52+72+…+232)+(32+62+92+…+242)=-
 (12+22+32+…+242)+
(12+22+32+…+242)+ (32+62+92+…+242)
(32+62+92+…+242)=-
 ×
×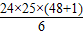 +
+ ×1835
×1835=-2450+2754
=304;
故选C;
点评:考查学生会求数列的和,掌握三角函数周期的计算方法,计算量比较大,考查学生的计算能力,是一道中档题;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目