题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则称
,则称![]() 是“紧密数列”.
是“紧密数列”.
(1)若数列![]() 是“紧密数列”,且
是“紧密数列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 为等差数列,首项
为等差数列,首项![]() ,公差
,公差![]() ,且
,且![]() ,判断
,判断![]() 是否为“紧密数列”,并说明理由;
是否为“紧密数列”,并说明理由;
(3)设数列![]() 是公比为
是公比为![]() 的等比数列,若数列
的等比数列,若数列![]() 与
与![]() 都是“紧密数列”,求
都是“紧密数列”,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 是“紧密数列”,详见解析(3)
是“紧密数列”,详见解析(3)![]()
【解析】
(1)由 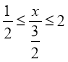 ,
,![]() 可求出
可求出![]() 的取值范围;
的取值范围;
(2)由![]() ,所以
,所以![]()
![]()
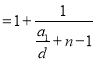
![]() ,根据“紧密数列”的定义即可得到结论;
,根据“紧密数列”的定义即可得到结论;
(3)根据”![]() 是紧密函数”可得
是紧密函数”可得![]() ,再对
,再对![]() 分
分![]() 三种情况套,结合“紧密数列”的定义可得.
三种情况套,结合“紧密数列”的定义可得.
(1)由题意得: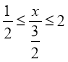 ,
,![]() ,解得
,解得![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.
(2)由题意得![]() ,所以
,所以![]()
![]()
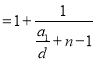
![]() ,
,
因为![]() 随着
随着![]() 的增大而减小,所以
的增大而减小,所以![]() 时,
时,![]() 取得最大值,所以
取得最大值,所以 ,
,
所以![]() 是“紧密数列”.
是“紧密数列”.
(3)由数列![]() 是公比为
是公比为![]() 的等比数列,得
的等比数列,得![]() ,
,
因为![]() 是“紧密数列”,所以
是“紧密数列”,所以![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() 时,数列
时,数列![]() 为“紧密数列”,故
为“紧密数列”,故![]() 满足题意.
满足题意.
②当![]() 时,
时,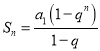 ,则
,则![]() ,因为数列
,因为数列![]() 为“紧密数列”,
为“紧密数列”,
所以![]() ,对任意
,对任意![]() 恒成立.
恒成立.
(i)当![]() 时,
时,![]() ,
,
即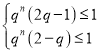 ,对任意
,对任意![]() 恒成立.
恒成立.
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以,当![]() 时,
时,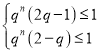 ,对任意
,对任意![]() 恒成立.
恒成立.
(ii)当![]() 时,
时,![]() ,即
,即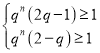 ,对任意
,对任意![]() 恒成立.
恒成立.
所以当![]() 时,有
时,有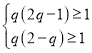 成立,即
成立,即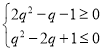 ,所以
,所以![]() 且
且![]() ,
,
所以![]() ,这与
,这与![]() 相矛盾,此时
相矛盾,此时![]() 不存在.
不存在.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.

【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)设![]() ,若对一切正整数
,若对一切正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;.
的取值范围;.
(3)是否存在正整数![]() ,使得
,使得![]() 。成等比数列?若存在,求出所有的
。成等比数列?若存在,求出所有的![]() ;若不存在,说明理由.
;若不存在,说明理由.
【题目】某租车公司给出的财务报表如下:
年度 项目 | 2014年 (1-12月) | 2015年 (1-12月) | 2016年 (1-11月) |
接单量(单) | 14463272 | 40125125 | 60331996 |
油费(元) | 214301962 | 581305364 | 653214963 |
平均每单油费 | 14.82 | 14.49 | |
平均每单里程 | 15 | 15 | |
每公里油耗 | 0.7 | 0.7 | 0.7 |
有投资者在研究上述报表时,发现租车公司有空驶情况,并给出空驶率的计算公式为![]() .
.
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里).