题目内容
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)设![]() ,若对一切正整数
,若对一切正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;.
的取值范围;.
(3)是否存在正整数![]() ,使得
,使得![]() 。成等比数列?若存在,求出所有的
。成等比数列?若存在,求出所有的![]() ;若不存在,说明理由.
;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不存在.
;(3)不存在.
【解析】
(1)由已知条件利用等差数列的通项公式和前![]() 项和公式列出方程组,求出首项和公差,由此能求出数列
项和公式列出方程组,求出首项和公差,由此能求出数列![]() 的前
的前![]() 项和;
项和;
(2)当![]() 为偶数时,设
为偶数时,设![]() ,
,![]() ,求出
,求出![]() ,进而求出
,进而求出![]() ;当
;当![]() 为奇数时,设
为奇数时,设![]() ,
,![]() ,求出
,求出![]() ,进而求出
,进而求出![]() ,由此能求出
,由此能求出![]() 的取值范围;
的取值范围;
(3)假设存在正整数![]() ,
,![]()
![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列,由此利用已知条件推导出等式
成等比数列,由此利用已知条件推导出等式![]() 不成立,从而得到不存在正整数
不成立,从而得到不存在正整数![]() ,
,![]()
![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)设数列![]() 的公差为
的公差为![]() .
.
![]()
![]() ,
,![]() ,
,
![]()
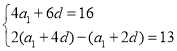 ,解得
,解得![]() ,
,![]() ,
,
![]()
![]() ;
;
(2)当![]() 为偶数时:
为偶数时:![]() ,不等式
,不等式
![]() 分离参数得到
分离参数得到![]() 研究右边函数性质,
研究右边函数性质,
此为单调递增,所以![]()
当![]() 为奇数时:
为奇数时:![]() ,不等式
,不等式
![]() ,从而
,从而![]()
综上:![]() ;
;
(3)假设存在正整数![]() ,
,![]() (
(![]() ),使得/span>
),使得/span>![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,
则![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
即![]() .
.
![]()
![]() ,
,![]()
![]() ,
,![]() ,∴
,∴![]() .
.
![]()
![]() 是整数,
是整数,![]() 等式
等式![]() 不成立,
不成立,
故不存在正整![]() ,
,![]()
![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.

练习册系列答案
相关题目