题目内容

【题目】设函数由方程确定，下列结论正确的是________（请将你认为正确的序号都填上）

① 是上的单调递减函数；

② 对于任意，恒成立；

③ 对于任意，关于的方程都有解；

④ 存在反函数，且对任意，总有成立.

【答案】①②③④

【解析】

首先化简所给的方程，画出其对应的图像，然后逐一考查所给的结论是否正确即可.

方程等价于：

，

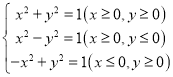绘制其对应的曲线如图所示：

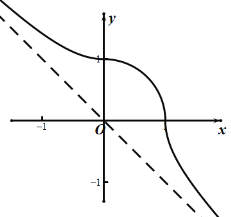
据此考查所给的性质：

① 由函数图像可知是上的单调递减函数；

② 注意到两段双曲线的渐近线均为，

故对于任意，恒成立；

③ 很明显函数的值域为R，故对于任意，关于的方程都有解；

④ 很明显单调递减函数的定义域、值域均为，且函数关于直线对称，

故存在反函数，且对任意，总有成立.

综上可得，结论正确的是①②③④.

故答案为：①②③④．

练习册系列答案
相关题目

【题目】某文体局为了解“跑团”每月跑步的平均里程，收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程（单位：公里）的数据，绘制了下面的折线图.根据折线图，下列结论正确的是（ ）

A. 月跑步平均里程的中位数为6月份对应的里程数

B. 月跑步平均里程逐月增加

C. 月跑步平均里程高峰期大致在8、9月

D. 1月至5月的月跑步平均里程相对于6月至11月，波动性更小，变化比较平稳

【题目】设数列的前项和为，若，则称是“紧密数列”.

（1）若数列是“紧密数列”，且，，，，求的取值范围；

（2）若为等差数列，首项，公差，且，判断是否为“紧密数列”，并说明理由；

（3）设数列是公比为的等比数列，若数列与都是“紧密数列”，求的取值范围.

【题目】已知（

（1）当a＝0时，求f（x）的极值；

（2）当a＞0时，讨论f（x）的单调性；

（3）若对任意的a∈（2, 3），x1, x2∈[1, 3]，恒有（m－ln3）a－2ln3＞|f（x1）－f（x2）|成立，求实数m的取值范围.

【题目】在平面直角坐标系中，直线与圆相切，圆心的坐标为．

（1）求圆的方程；

（2）设直线与圆没有公共点，求的取值范围；

（3）设直线与圆交于、两点，且，求的值．

【题目】已知函数是奇函数，且时，有，，则不等式的解集为____．

【题目】在平面直角坐标系中，已知双曲线分别为的左，右顶点.

(1)以为圆心的圆与恰有三个不同的公共点，写出此圆的方程；

(2)直线过点,与在第一象限有公共点,线段的垂直平分线过点,求直线的方程；

(3)上是否存在异于点,使成立，若存在，求出所有的坐标，若不存在说明理由.

【题目】已知常数，数列满足，.

(1)若，，求的值；

(2)在(1)的条件下，求数列的前项和；

(3)若数列中存在三项，，(且)依次成等差数列,求的取值范围.

【题目】记无穷数列的前项中最大值为，最小值为，令，.

（1）若，请写出的值；

（2）求证：“数列是等差数列”是“数列是等差数列”的充要条件；

（3）若对任意，有，且，请问：是否存在，使得对于任意不小于的正整数，有成立？请说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网