题目内容
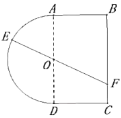
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,以线段
,以线段![]() 为直径的圆与椭圆交于点
为直径的圆与椭圆交于点 .
.

(1)求椭圆的方程;
(2)过![]() 轴正半轴上一点
轴正半轴上一点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() .
.
①若![]() 与圆和椭圆都相切,求实数
与圆和椭圆都相切,求实数![]() 的值;
的值;
②直线![]() 在
在![]() 轴左侧交圆于
轴左侧交圆于![]() 、
、![]() 两点,与椭圆交于点
两点,与椭圆交于点![]() 、
、![]() (从上到下依次为
(从上到下依次为![]() 、
、![]() 、
、![]() 、
、![]() ),且
),且![]() ,求实数
,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]() 的最大值为3
的最大值为3
【解析】
(1)线段![]() 为直径的圆与椭圆交于点
为直径的圆与椭圆交于点![]() ,可以得圆的方程及
,可以得圆的方程及![]() ,将点
,将点![]() 代入椭圆方程得
代入椭圆方程得![]() ,又因为
,又因为![]() ,就可解出
,就可解出![]() ,
,![]() ,进而得出椭圆方程.
,进而得出椭圆方程.
(2)①设直线![]() 的方程为:
的方程为:![]() ,即
,即![]() ,因为
,因为![]() 与圆和椭圆相切,得
与圆和椭圆相切,得![]() ,△
,△![]() ,解得,
,解得,![]() ,
,![]() .
.
②取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,又
,又![]() ,所以点
,所以点![]() 为
为![]() 中点,写出
中点,写出![]() 点坐标,进而得
点坐标,进而得![]() 坐标,代入椭圆方程化简得,
坐标,代入椭圆方程化简得,![]() ,设
,设![]() ,最后再求则
,最后再求则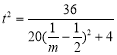 最值.
最值.
解:(1)设椭圆的焦距为![]()
因为线段![]() 为直径的圆与椭圆交于点
为直径的圆与椭圆交于点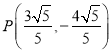
所以![]()
又点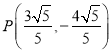 在椭圆上
在椭圆上
所以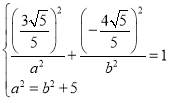 ,解得
,解得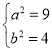
所以椭圆的方程为![]()
(2)①因为直线![]() 与圆相切,所以
与圆相切,所以![]() ,即
,即![]() (ⅰ)
(ⅰ)
由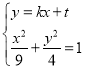 ,消去
,消去![]() 得
得![]()
因为直线与椭圆相切,
所以![]() 即
即![]() (ⅱ)
(ⅱ)
联立(i)(ⅱ)得![]() 负值舍去
负值舍去
②取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() 为
为![]() 中点
中点
由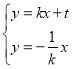 ,解得
,解得![]()
所以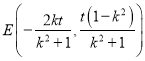
代入椭圆方程化简得
设![]()
则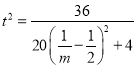 ,当
,当![]() 时,
时,![]() 取最大值3,此时
取最大值3,此时![]() .
.
又![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
符合题意,故![]() 的最大值为3.
的最大值为3.

练习册系列答案
相关题目