题目内容
13.给出如下四个命题:①命题p:?x0∈R,x${\;}_{0}^{2}$+x0-1<0,则非p:?x∉R,x2+x-1≥0;
②命题“若x≥2且y≥3,则x+y≥5”的否命题为“若x<2且y<3,则x+y<5”;
③四个实数a,b,c,d依次成等比数列的必要而不充分条件是ad=bc;
④在△ABC中,“A>45°”是“sinA>$\frac{\sqrt{2}}{2}$”的充分不必要条件
其中正确的命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据含有量词的命题的否定进行判断.
②根据否命题的定义进行判断,
③由等比数列的性质,实数a、b、c、d依次成等比数列⇒ad=bc,反之,举出反例,判断即可;进而可判断其正确与否;
④根据充分不必要条件进行判断.
解答 解:①命题p:?x0∈R,x${\;}_{0}^{2}$+x0-1<0,则非p:?x∈R,x2+x-1≥0;正确,故①错误,
②命题“若x≥2且y≥3,则x+y≥5”的否命题为“若x<2或y<3,则x+y<5”;故②错误,
③由等比数列的性质,实数a、b、c、d依次成等比数列⇒ad=bc,
反之,若a=0,c=0,ad=bc=0,但实数a、b、c、d不符合等比数列的定义,
故四个实数a、b、c、d依次成等比数列的必要而不充分条件是ad=bc,正确;故③正确,
④若A=150°>45°,则sinA=$\frac{1}{2}$<$\frac{\sqrt{3}}{2}$,即“A>45°”不是“$sinA>\frac{{\sqrt{2}}}{2}$”的充分条件,错误;故④错误,
故选:A
点评 本题考查命题真假的判断,涉及复合命题真假的判断、四种命题、充分必要条件的判断等知识点,是基础类型的题目,难度不大.

练习册系列答案
相关题目
3.幂函数的图象过点$(2,\sqrt{2})$,则该幂函数的解析式为( )
| A. | y=x-1 | B. | $y={x^{\frac{1}{2}}}$ | C. | y=x2 | D. | y=x3 |

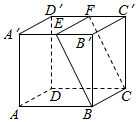 如图,在正方体中,E,F是棱A′B′与D′C′的中点,求面EBCF与面ABCD所成二面角的正切值.(取锐角)
如图,在正方体中,E,F是棱A′B′与D′C′的中点,求面EBCF与面ABCD所成二面角的正切值.(取锐角)