题目内容
17.△ABC中,内角A,B,C所对的边分别是a,b,c,已知sinAsinB=sinCtanC.(1)求$\frac{{a}^{2}{+b}^{2}}{{c}^{2}}$的值:
(2)若a=$\frac{\sqrt{2}}{2}$c,且△ABC的面积为4,求c的值.
分析 (1)利用sinAsinB=sinCtanC,根据正、余弦定理,即可求$\frac{{a}^{2}{+b}^{2}}{{c}^{2}}$的值:
(2)若a=$\frac{\sqrt{2}}{2}$c,求出b,sinC,利用△ABC的面积为4,求c的值.
解答 解:(1)∵sinAsinB=sinCtanC,
∴ab=$\frac{{c}^{2}•2ab}{{a}^{2}+{b}^{2}-{c}^{2}}$,
∴a2+b2=3c2,
∴$\frac{{a}^{2}{+b}^{2}}{{c}^{2}}$=3;
(2)∵a=$\frac{\sqrt{2}}{2}$c,a2+b2=3c2,
∴b=$\frac{\sqrt{10}}{2}$c,
∴cosC=$\frac{\frac{1}{2}{c}^{2}+\frac{5}{2}{c}^{2}-{c}^{2}}{2•\frac{\sqrt{2}}{2}c•\frac{\sqrt{10}}{2}c}$=$\frac{2\sqrt{5}}{5}$,
∴sinC=$\frac{1}{\sqrt{5}}$,
∵△ABC的面积为4,
∴$\frac{1}{2}$•$\frac{\sqrt{2}}{2}$c•$\frac{\sqrt{10}}{2}$c•$\frac{1}{\sqrt{5}}$=4,
∴c=4.
点评 本题考查正、余弦定理,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
7.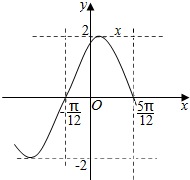 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )| A. | $\sqrt{3}$ | B. | 0 | C. | -2 | D. | 1 |
8.过点($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),且与圆x2+y2=1相切的直线方程是( )
| A. | y=x+$\sqrt{2}$ | B. | y=-x+$\sqrt{2}$ | C. | y=x-$\sqrt{2}$ | D. | y=-x-$\sqrt{2}$ |