题目内容
已知椭圆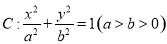 的离心率
的离心率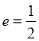 ,点A为椭圆上一点,
,点A为椭圆上一点,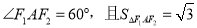 .
.
(1)求椭圆C的方程;
(2)设动直线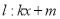 与椭圆C有且只有一个公共点P,且与直线
与椭圆C有且只有一个公共点P,且与直线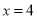 相交于点Q.问:在
相交于点Q.问:在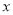 轴上是否存在定点M,使得以PQ为直径的圆恒过定点M?若存在,求出点M的坐标;若不存在,说明理由.
轴上是否存在定点M,使得以PQ为直径的圆恒过定点M?若存在,求出点M的坐标;若不存在,说明理由.
(1)椭圆C的方程为 ;(2)存在定点M,坐标为(1,0).
;(2)存在定点M,坐标为(1,0).
【解析】
试题分析:(1)由 可得
可得 ,①
,①
 ,可得
,可得 , 2分
, 2分
在 中由余弦定理可得:
中由余弦定理可得: ,又
,又 ,
,
可得 ,② 4分
,② 4分
联立①②得: ,∴
,∴ ,
,
∴椭圆的方程为 ; 6分
; 6分
(2)设点P .由
.由 ,得
,得 , 8分
, 8分
 ,化简得
,化简得 ,
,
∴ , 10分
, 10分
∴P .
.
由 ,得Q(4,4k+m),假设存在点M,坐标为
,得Q(4,4k+m),假设存在点M,坐标为 ,
,
则 ,
, . 12分
. 12分
∵以PQ为直径的圆恒过M点,∴ ,即
,即 ,
,
∴ 对任意k,m都成立.
对任意k,m都成立.
则 ,解得
,解得 ,故存在定点M(1,0)符合题意. 14分
,故存在定点M(1,0)符合题意. 14分
考点:考查了椭圆的标准方程,直线与椭圆的位置关系,直线过定点问题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
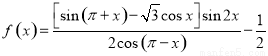 .
.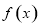 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;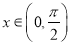 时,求
时,求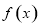 的最大值,并求此时对应的
的最大值,并求此时对应的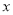 的值.
的值.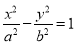 的焦点到其渐近线的距离等于2,抛物线
的焦点到其渐近线的距离等于2,抛物线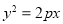 的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为4,则抛物线方程为
的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为4,则抛物线方程为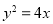 B.
B.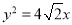 C.
C.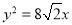 D.
D.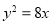
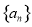 满足
满足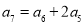 ,若存在不同的两项
,若存在不同的两项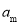 和
和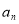 ,使得
,使得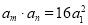 ,则
,则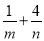 的最小值是__________.
的最小值是__________. 与
与 的方程分别为
的方程分别为 与
与 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,则曲线
轴的正半轴,建立平面直角坐标系,则曲线 与
与 交点的直角坐标为 .
交点的直角坐标为 .