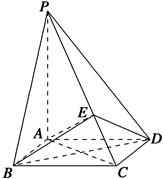
题目内容
如图,棱柱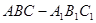 中,四边形
中,四边形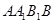 是菱形,四边形
是菱形,四边形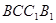 是矩形,
是矩形,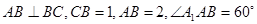 .
.
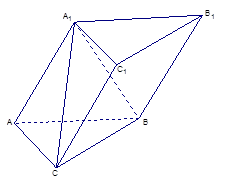
(1)求证:平面 ;
;
(2)求点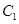 到平面
到平面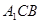 的距离;
的距离;
(3)求直线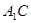 与平面
与平面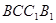 所成角的正切值.
所成角的正切值.
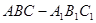 中,四边形
中,四边形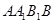 是菱形,四边形
是菱形,四边形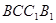 是矩形,
是矩形,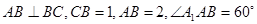 .
.
(1)求证:平面
 ;
;(2)求点
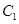 到平面
到平面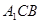 的距离;
的距离;(3)求直线
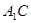 与平面
与平面 所成角的正切值.
所成角的正切值. (1)证明过程详见试题解析;(2)点 到平面
到平面 的距离为
的距离为 ;(3)直线
;(3)直线 与平面
与平面 所成角的正切值为
所成角的正切值为 .
.
 到平面
到平面 的距离为
的距离为 ;(3)直线
;(3)直线 与平面
与平面 所成角的正切值为
所成角的正切值为 .
.试题分析:(1)先证明
 面
面 ,又
,又 面
面 ,∴平面
,∴平面 ;(2)先求出
;(2)先求出 ,即可知点
,即可知点 到面
到面 的距离,而点
的距离,而点 到面
到面 的距离相等,所以点
的距离相等,所以点 到平面
到平面 的距离为
的距离为 ;(3)先找出
;(3)先找出 在面
在面 的射影
的射影 ,
, 为直线
为直线 与平面
与平面 所成线面角,放在
所成线面角,放在 中即可求出直线
中即可求出直线 与平面
与平面 所成角的正切值为
所成角的正切值为 .
.试题解析:(1)
 4分
4分(2)解:
 面
面 ,所以点
,所以点 到面
到面 的距离相等, 6分
的距离相等, 6分设点
 到面
到面 的距离相等,则
的距离相等,则
∵
 ,∴
,∴ 为正三角形,
为正三角形,
 7分
7分又
 8分
8分
∴
 ,∴
,∴ ,点
,点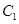 到平面
到平面 的距离为
的距离为 . 9分
. 9分(3)解:过
 作
作 ,垂足为
,垂足为 10分
10分 面
面 12分
12分∴
 为
为 在面
在面 的射影,
的射影, 为直线
为直线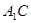 与平面
与平面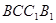 所成线面角, 13分
所成线面角, 13分在
 中,
中, ,
,所以直线
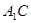 与平面
与平面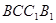 所成角的正切值为
所成角的正切值为 . 14分
. 14分
练习册系列答案
相关题目
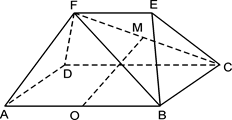
 中,底面
中,底面 是正方形,侧面
是正方形,侧面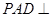 底面
底面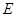 ,
, 分别为
分别为 ,
, 中点,求证:
中点,求证: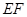 ∥平面
∥平面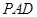 ;
;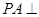
 ;
;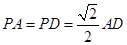 ,求证:平面
,求证:平面 平面
平面 .
.
 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.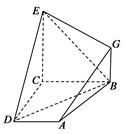
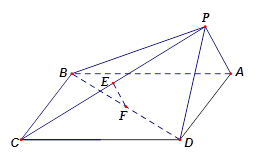
 底面
底面 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形, ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.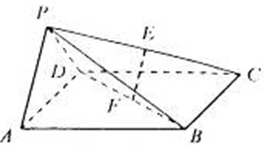
 平面
平面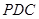 .
. α,则m//α
α,则m//α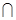 β="m," n⊥m ,则n⊥α.
β="m," n⊥m ,则n⊥α.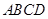 沿对角线
沿对角线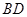 折成直二面角
折成直二面角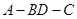 ,有如下四个结论:
,有如下四个结论: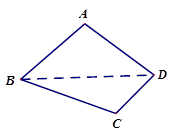
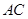 ⊥
⊥ 是等边三角形;
是等边三角形;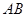 与
与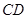 所成的角为60°;
所成的角为60°; 所成的角为60°.
所成的角为60°.