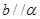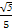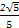题目内容
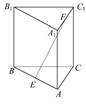
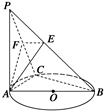
已知多面体ABCDFE中, 四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M分别为AB、FC的中点,且AB = 2,AD =" EF" = 1.
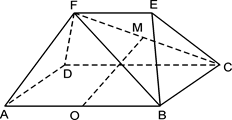
(1)求证:AF⊥平面FBC;
(2)求证:OM∥平面DAF;
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE的值.

(1)求证:AF⊥平面FBC;
(2)求证:OM∥平面DAF;
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE的值.
(1)(2)见解析(3)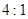
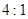
试题分析:(1)要证
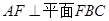 ,则需要证明
,则需要证明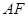 与平面
与平面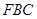 内的两条相交直线垂直,而根据题意已知
内的两条相交直线垂直,而根据题意已知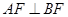 ,故只需再根据题意平面
,故只需再根据题意平面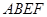 ⊥平面
⊥平面 ,可证
,可证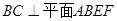 ,从而证明
,从而证明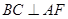 ,则可证明结论.
,则可证明结论.(2)要证
 ∥平面
∥平面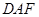 ,则需要在平面
,则需要在平面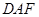 内找一条直线与
内找一条直线与 平行,根据点
平行,根据点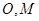 都是中点的特点, 取
都是中点的特点, 取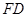 中点
中点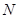 ,证明四边形
,证明四边形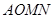 为平行四边形,即有
为平行四边形,即有 ∥
∥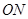 ,则可证明结论.
,则可证明结论.(3)要求体积比,首先得找到体积,根据题意可知,分割后形成了两个棱锥,一个四棱锥,一个三棱锥;根据棱锥的体积公式,得找到底面积和高,而其中四棱锥的底面和高比较容易确定,而三棱锥中关键是确定底面和高,确定的依据就是是否有现成的线面垂直,显然
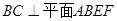 ,所以确定底面为
,所以确定底面为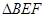 高
高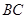 .最后分别求体积做比值即可.
.最后分别求体积做比值即可.试题解析:(1)
 平面
平面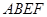 ⊥平面
⊥平面 ,平面
,平面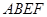
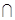 平面
平面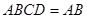 ,
,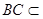 平面
平面 ,而四边形
,而四边形 为矩形
为矩形 ,
,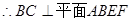
.
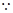
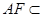 平面
平面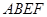
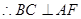
则
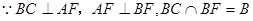 ,
,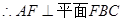
(2)取
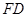 中点
中点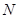 ,连接
,连接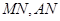 ,则
,则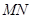 ∥
∥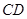 ,且
,且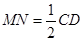 ,又四边形
,又四边形 为矩形,
为矩形,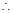
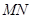 ∥
∥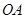 ,且
,且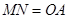
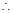 四边形
四边形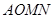 为平行四边形,
为平行四边形,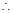
 ∥
∥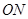
又
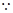

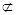 平面
平面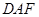 ,
,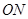
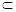 平面
平面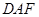
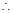
 ∥平面
∥平面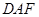
(3)过
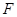 作
作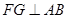 于
于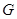 ,由题意可得:
,由题意可得: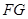
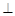 平面
平面 .
.所以:
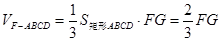 .
.因为
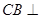 平面
平面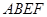 , 所以
, 所以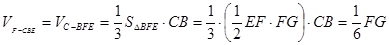
所以

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
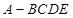 ,
,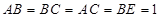 ,
,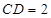 ,
,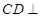 平面
平面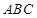 ,
,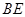 ∥
∥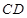 ,
,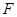 为
为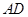 的中点.
的中点.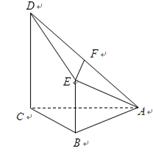
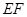 ∥平面
∥平面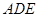
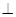 平面
平面 ;
;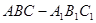 中,四边形
中,四边形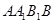 是菱形,四边形
是菱形,四边形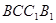 是矩形,
是矩形,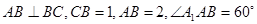 .
.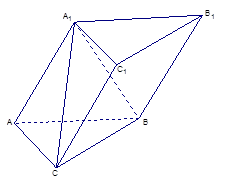
 ;
;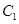 到平面
到平面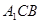 的距离;
的距离;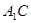 与平面
与平面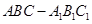 中,点
中,点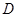 是
是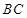 上一点.
上一点.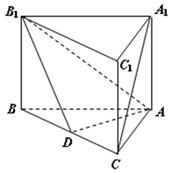
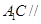 平面
平面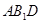 ;
;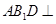 平面
平面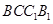 ,求证
,求证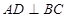 .
.
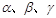 为平面,
为平面,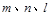 为直线,以下四组条件,可以作为
为直线,以下四组条件,可以作为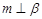 的一个充分条件的是( )
的一个充分条件的是( )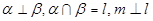
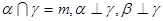
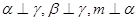
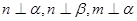
 是两条不同的直线,
是两条不同的直线,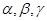 是三个不同的平面,则下列命题正确的是( )
是三个不同的平面,则下列命题正确的是( )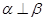 ,
,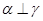 ,则
,则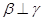
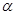 所成的角相等,则
所成的角相等,则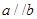
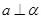 ,
,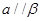 ,则
,则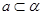 ,则
,则