Question

已知函数y=x²+bx+c(b、c是常数)，是否存在常数b与c，使得当x≤1时，x²+bx+c≥0,并且当1≤x≤3时，x²+bx+c≤0恒成立？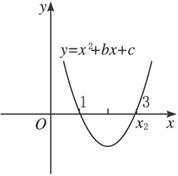

Answer 1

解：假设存在b、c，由已知x=1时，x²+bx+c=0,即x=1是方程x²+bx+c=0一根，设另一根为x₂，由已知{x|x²+bx+c≤0}={x|1≤x≤x₂}{x|1≤x≤3}，

∴1+x₂≥1+3,

∴-b≥4

∴b≤-4.

又x=1时x²+bx+c=1+b+c=0,

∴b=-1-c≤-4,c≥3,

即b的范围是{b|b≤-4},c的范围是{c|c≥3}.