Question

【题目】已知等差数列满足，前8项和．

（1）求数列的通项公式；

（2）若数列满足．

① 证明：为等比数列；

② 求集合．

Answer 1

【答案】（1）（2）①见解析，②

【解析】

（1）设等差数列{an}的公差为d．根据a4＝4，前8项和S8＝36．可得数列{an}的通项公式；

（2）①设数列{bn}前n项的和为Bn．根据bn＝Bn﹣Bn﹣1，数列{bn}满足．建立关系即可求解；

②由，得，即．记，由①得，，

由，得cm＝3cp＞cp，所以m＜p；设t＝p﹣m（m，p，t∈N*），由，得．讨论整数成立情况即可；

（1）设等差数列的公差为d．

因为等差数列满足，前8项和，

所以，解得

所以数列的通项公式为．

（2）①设数列前项的和为．

由（1）及

得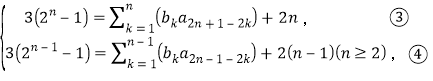

由③-④得

3

-

=

-

．

所以 ，

又，所以，满足上式．

所以

当时，

由⑤-⑥得，．

，

所以，，

所以数列是首项为1，公比为2的等比数列．

②由，得，即．

记，由①得，，

所以，所以（当且仅当时等号成立）．

由，得，

所以．

设 ，由，得．

当时，，不合题意；

当时，，此时符合题意；

当时，，不合题意；

当时，，不合题意．

下面证明当时，．

不妨设 ，

，

所以在上单调增函数，

所以，

所以当时，，不合题意．

综上，所求集合 ．