题目内容
已知正三角形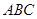 的边长为1,点
的边长为1,点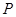 是
是 边上的动点,点
边上的动点,点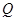 是
是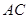 边上的动点,且
边上的动点,且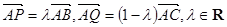 ,则
,则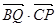 的最大值为
的最大值为
A.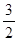 | B.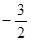 | C.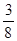 | D.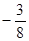 |
D
解析试题分析: ,
, ,
,

而 ,
, ,
, ,
, ,故当
,故当 时,
时, 取最大值
取最大值 .
.
考点:平面向量的减法、平面向量的数量积、二次函数

练习册系列答案
相关题目
已知向量 ,
, ,如果向量
,如果向量 与
与 垂直,则
垂直,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知| |=3,|
|=3,| |=5,且
|=5,且 ,则向量
,则向量 在向量
在向量 上的投影为( )
上的投影为( )
A. | B.3 | C.4 | D.5 |
在△ABC中, ,
, ,则△ABC的面积为( )
,则△ABC的面积为( )
| A.3 | B.4 | C.6 | D. |
已知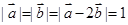 ,则
,则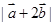 =( )
=( )
| A.9 | B.3 | C.1 | D.2 |
平面向量 与
与 夹角为60°,
夹角为60°, ,
, ,则
,则 ( )
( )
A. | B.12 | C.4 | D.2 |
定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b= mq
-np,下面说法错误的是( )
| A.若a与b共线,则a⊙b =0 | B.a⊙b =b⊙a |
C.对任意的 R,有( R,有( a)⊙b = a)⊙b = (a⊙b) (a⊙b) | D.(a⊙b)2+(a·b)2= |a|2|b|2 |
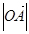 =1,
=1,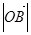 =
=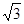 ,
,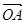 ·
·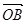 =0,点C在∠AOB内,且∠AOC=60°,设
=0,点C在∠AOB内,且∠AOC=60°,设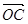 =m
=m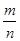 =( )
=( )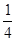
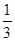
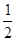
 |=1,|
|=1,| |=
|= ,
, =m
=m 等于( )
等于( )
