题目内容
复数z满足(z-i)(2-i)=5,则复数z在复平面内对应的点位于第 象限.
考点:复数的代数表示法及其几何意义
专题:计算题,数系的扩充和复数
分析:由(z-i)(2-i)=5,可求得z,由z对应的点的坐标可得答案.
解答:
解:由(z-i)(2-i)=5,得z=
+i=
+i=2+2i,
对应的点为(2,2),位于第一象限,
故答案为:一.
| 5 |
| 2-i |
| 5(2+i) |
| (2-i)(2+i) |
对应的点为(2,2),位于第一象限,
故答案为:一.
点评:该题考查复数代数形式的乘除运算、复数的几何意义,属基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知i是虚数单位,z=1+i,
为z的共轭复数,则复数
在复平面上对应的点的坐标为( )
. |
| z |
| z2 | ||
|
| A、(1,1) |
| B、(-1,-1) |
| C、(-1,1) |
| D、(1,-1) |
已知f(x)=
,则f(5)=( )
| x+2 |
| x-6 |
| A、-8 | B、-7 | C、-6 | D、-5 |
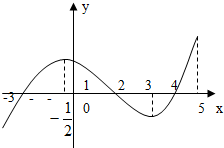 如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断: