题目内容
已知E、F分别在正方体ABCD-A1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC所成的二面角的正切值等于______.

由题意画出图形如图:
因为E、F分别在正方体ABCD-A1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1,
延长CB、FE交点为S连接AS,过B作BP⊥AS连接PE,所以面AEF与面ABC所成的二面角就是∠BPE,因为B1E=2EB,CF=2FC1,
所以BE:CF=1:2
所以SB:SC=1:2,
设正方体的棱长为:a,所以AS=
| 2 |
| ||
| 2 |
| a |
| 3 |
| BE |
| PB |
| ||||
|
| ||
| 3 |
故答案为:
| ||
| 3 |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
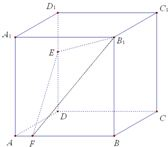 8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( )
8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( ) 求证:EF∥平面BB1C1C.
求证:EF∥平面BB1C1C.
