题目内容
(本小题满分12分)
在四棱柱 中,底面
中,底面 是直角梯形,AB∥CD,∠ABC=
是直角梯形,AB∥CD,∠ABC= ,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD
,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD

(1)求证:AB⊥平面PBC
(2)求三棱锥C-ADP的体积
(3)在棱PB上是否存在点M使CM∥平面PAD?
若存在,求 的值。若不存在,请说明理由。
的值。若不存在,请说明理由。
在四棱柱
 中,底面
中,底面 是直角梯形,AB∥CD,∠ABC=
是直角梯形,AB∥CD,∠ABC= ,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD
,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD
(1)求证:AB⊥平面PBC
(2)求三棱锥C-ADP的体积
(3)在棱PB上是否存在点M使CM∥平面PAD?
若存在,求
 的值。若不存在,请说明理由。
的值。若不存在,请说明理由。(1)证明:因为∠ABC= ,所以AB⊥BC。因为平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AB
,所以AB⊥BC。因为平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AB 平面ABCD,所以AB⊥平面PBC ;(2)
平面ABCD,所以AB⊥平面PBC ;(2) ;(3)在棱PB上存在点M使得CM∥平面PAD,此时
;(3)在棱PB上存在点M使得CM∥平面PAD,此时
 ,所以AB⊥BC。因为平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AB
,所以AB⊥BC。因为平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AB 平面ABCD,所以AB⊥平面PBC ;(2)
平面ABCD,所以AB⊥平面PBC ;(2) ;(3)在棱PB上存在点M使得CM∥平面PAD,此时
;(3)在棱PB上存在点M使得CM∥平面PAD,此时
试题分析:(1)证明:因为∠ABC=
 ,所以AB⊥BC。 (1分)
,所以AB⊥BC。 (1分)因为平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC
AB
 平面ABCD,所以AB⊥平面PBC (4分)
平面ABCD,所以AB⊥平面PBC (4分)(2)取BC的中点O,连接PO
因为PB=PC,所以PO⊥BC
因为平面PBC⊥平面ABCD
平面PBC∩平面ABCD=BC,PO
 平面PBC
平面PBC所以PO⊥平面ABCD (5分)
 在等边△PBC中PO=
在等边△PBC中PO=

 (8分)
(8分)(3)在棱PB上存在点M使得CM∥平面PAD,此时

 证明:取AB的中点N,连接CM,CN,MN
证明:取AB的中点N,连接CM,CN,MN则MN∥PA,AN=

因为AB ="2CD" 所以AN=CD
因为AB ∥CD所以四边形ANCD是平行四边形。
所以CN∥AD
因为MN∩CN=N,PA∩AD=A
所以平面MNC∥平面PAD (10分)
因为
 平面MNC
平面MNC所以CM∥平面PAD ( 12分)
点评:以棱锥柱为载体考查立体几何中的线面、面面、点面位置关系或距离是高考的亮点,掌握其判定性质及定理,是解决此类问题的关键

练习册系列答案
相关题目
 ,
, 是两条不同的直线,
是两条不同的直线, ,
, ,
, 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题: ,
, ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ;
; ,
, ,
, ;④ 若
;④ 若 ,
, ,
, 、
、 是不同的直线,
是不同的直线, 、
、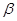 、
、 是不同的平面,有以下四命题:
是不同的平面,有以下四命题:  ,则
,则 ; ②若
; ②若 ,则
,则 ;
; ,则
,则 ; ④若
; ④若 ,则
,则 .
. 的底面为菱形,且
的底面为菱形,且 ,
,
 ,
, 为
为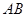 的中点.
的中点.

 平面
平面 ;
; 到面
到面 的距离.
的距离. 、
、 ,能判定
,能判定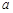

 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: ,则
,则 ②若
②若 则
则 ;
;  则
则 ; ④若
; ④若 则
则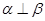 ;
;  中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,且
,且 ,
, 为
为 中点.
中点.
 平面
平面 的余弦值.
的余弦值. 中,底面
中,底面 是正方形.已知
是正方形.已知 ,
, .
.
 ;
; .
.


