题目内容
10.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为(1,0),且右焦点到上顶点的距离为$\sqrt{2}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)过点P(2,2)的动直线交椭圆C于A,B两点,
(i)若|PA||PB|=$\frac{20}{3}$,求直线AB的斜率;
(ii)点Q在线段AB上,且满足$\frac{1}{|PA|}$+$\frac{1}{|PB|}$=$\frac{2}{|PQ|}$,求点Q的轨迹方程.
分析 (Ⅰ)根据题意求出a,c的值,从而求出b的值,求出椭圆的方程即可;
(Ⅱ)(i)设出直线方程,和椭圆联立方程组,根据根与系数的关系求出直线斜率k的值即可;
(ii)设出Q的坐标,根据$\frac{1}{|PA|}$+$\frac{1}{|PB|}$=$\frac{2}{|PQ|}$,得$\frac{1}{2{-x}_{1}}$+$\frac{1}{2{-x}_{2}}$=$\frac{2}{2{-x}_{0}}$,求出k的值,带入直线方程,整理即可.
解答 解:(Ⅰ)由题意得:c=1,a=$\sqrt{2}$,
∴b2=a2-c2=1,
∴$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)(i)设直线AB:y=k(x-2)+2,
点A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}{+y}^{2}=1}\\{y=k(x-2)+2}\end{array}\right.$,
得:(1+2k2)x2+4k(2-2k)x+2(2-2k)2-2=0(*),
∴x1+x2=-$\frac{4k(2-2k)}{1+{2k}^{2}}$,x1x2=$\frac{{2(2-2k)}^{2}-2}{1+{2k}^{2}}$,
|PA||PB|=$\sqrt{1{+k}^{2}}$|2-x1|•$\sqrt{1{+k}^{2}}$|2-x2|
=(1+k2)[4-2(x1+x2)+x1x2]
=$\frac{10(1{+k}^{2})}{1+{2k}^{2}}$=$\frac{20}{3}$,
解得:k2=1,即k=1或-1;
(ii)设点Q(x0,y0),由点Q在直线AB上,
得y0=k(x0-2)+2,(**),
又$\frac{1}{|PA|}$+$\frac{1}{|PB|}$=$\frac{2}{|PQ|}$,得$\frac{1}{2{-x}_{1}}$+$\frac{1}{2{-x}_{2}}$=$\frac{2}{2{-x}_{0}}$,
∵$\frac{1}{2{-x}_{1}}$+$\frac{1}{2{-x}_{2}}$=$\frac{4-{(x}_{1}{+x}_{2})}{4-2{(x}_{1}{+x}_{2}){{+x}_{1}x}_{2}}$,
∴2-x0=2×$\frac{4-2{(x}_{1}{+x}_{2}){{+x}_{1}x}_{2}}{4-{(x}_{1}{+x}_{2})}$=2×(2+$\frac{{{x}_{1}x}_{2}-4}{4-{(x}_{1}{+x}_{2})}$)=$\frac{5}{1+2k}$,
∴k=$\frac{3{+x}_{0}}{2(2{-x}_{0})}$,
把它带入(**)式,得y0=k(x0-2)+2=$\frac{3{+x}_{0}}{2(2{-x}_{0})}$(x0-2)+2=-$\frac{1}{2}$x0+$\frac{1}{2}$,
即点Q的轨迹方程是:x+2y-1=0,($\frac{1-\sqrt{10}}{3}$<x<$\frac{1+\sqrt{10}}{3}$).
点评 本题考查了直线和椭圆的位置关系,考查考查椭圆的性质以及直线的斜率问题,是一道综合题.

| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{2}$,0) |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{7\sqrt{3}}{2}$ | D. | $\frac{8\sqrt{3}}{3}$ |
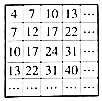 1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.
1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.