题目内容
6.已知定义域为R的函数y=g(x)满足以下条件:①?x∈R,g(3-x)=g(3+x);
②g(x)=g(x+2);
③当x∈[1,2]时,g(x)=-2x2+4x-2.
若方程g(x)=loga(x+1)(a>0,a≠1)在[0,+∞)上至少有5个不等的实根,则实数a的取值范围为( )
| A. | $({0,\frac{{\sqrt{3}}}{3}})$ | B. | $({0,\frac{{\sqrt{5}}}{3}}]$ | C. | $({0,\frac{{\sqrt{5}}}{5}})$ | D. | $[{\frac{1}{2},+∞})$ |
分析 根据条件判断函数的对称性和周期性,利用函数与方程的关系转化为两个数的图象交点个数问题,利用数形结合进行求解即可.
解答 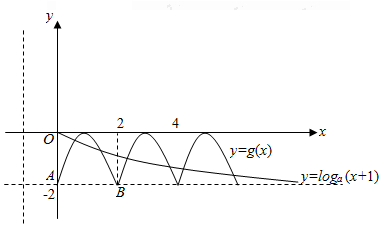 解:由g(3-x)=g(3+x),
解:由g(3-x)=g(3+x),
知即g(x)的图象
关于直线x=3对称,
由g(x)=g(x+2)知,
g(x)的一个周期T=2.
结合当x∈[1,2]时,
g(x)=-2x2+4x-2,
作出g(x)的图象与函数
y=loga(x+1)(x>0)的图象,
则方程g(x)=loga(x+1)在(0,+∞)上至少有5个不等的实根等价于
函数g(x)的图象与函数y=loga(x+1)(x>0)的图象至少有5个交点,
如图所示,则$\left\{\begin{array}{l}{0<a<1}\\{lo{g}_{a}(4+1)=lo{g}_{a}5>-2}\end{array}\right.$,
所以0<a<$\frac{\sqrt{5}}{5}$.
故选:C.
点评 本题主要考查函数与方程的应用,方程根的个数问题解法,根据条件判断函数的对称性和周期性,利用函数与方程之间的关系转化为两个函数的交点个数问题是解决本题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
19.任取一个自然数,则该数平方的末尾数是4的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于
的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于 的概率为( )
的概率为( ) B.
B.
 D.
D.
 的图象过点
的图象过点 ,则
,则 的值为( )
的值为( )
 D.
D.
 的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于
的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于 的概率为( )
的概率为( ) B.
B. C.
C. D.
D.