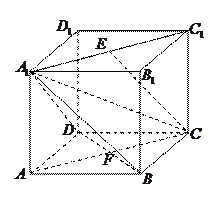题目内容
(本小题满分12分)
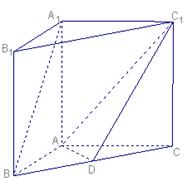
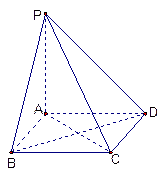
如图, 在直三棱柱ABC-A1B1C1中,AC=3 ,BC=4,
,BC=4,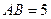 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求二面角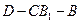 的余弦值.
的余弦值.
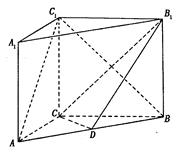
如图, 在直三棱柱ABC-A1B1C1中,AC=3
 ,BC=4,
,BC=4,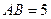 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求二面角
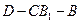 的余弦值.
的余弦值.
(1) 略
(2)
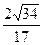
(Ⅰ)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
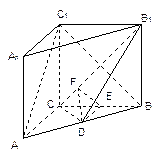
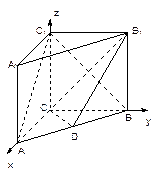
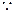
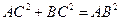
∴ AC⊥BC, …………………2分
又 AC⊥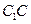 ,且
,且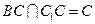
∴ AC⊥平面BCC1,又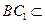 平面BCC1 ……………………………………4分
平面BCC1 ……………………………………4分
∴ AC⊥BC1 ………………………………………………………………5分
(Ⅱ)解法一:取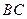 中点
中点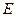 ,过
,过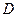 作
作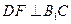 于
于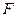 ,连接
,连接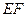 …………6分
…………6分
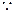
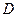 是
是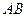 中点,
中点,
∴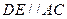 ,又
,又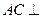 平面
平面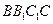
∴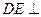 平面
平面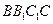 ,
,
又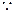
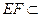 平面
平面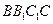 ,
,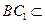 平面
平面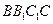
∴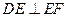
∴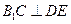 又
又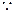
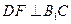 且
且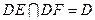
∴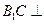 平面
平面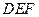 ,
,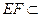 平面
平面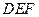 ………8分
………8分
∴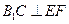 又
又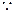
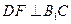
∴ 是二面角
是二面角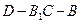 的平面角 ……………………………………10分
的平面角 ……………………………………10分
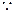 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,
∴在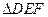 中,
中,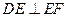 ,
,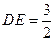 ,
,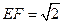
∴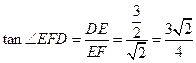 …………………………………………11分
…………………………………………11分
∴二面角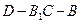 的正切值为
的正切值为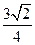 …………………………………………12分
…………………………………………12分
解法二:以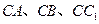 分别为
分别为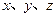 轴建立如图所示空间直角坐标系…………6分
轴建立如图所示空间直角坐标系…………6分
 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,
∴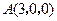 ,
,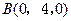
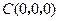 ,
,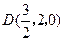 ,
,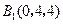 ,
,
∴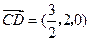 ,
,
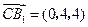
平面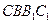 的法向量
的法向量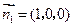 , …………………8分
, …………………8分
设平面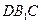 的法向量
的法向量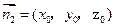 ,
,
则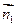 ,
,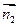 的夹角(或其补角)的大小就是二面角
的夹角(或其补角)的大小就是二面角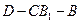 的大小 …………9分
的大小 …………9分
则由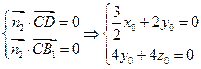 令
令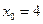 ,则
,则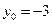 ,
,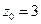 ∴
∴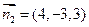 ………………10分
………………10分
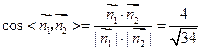 ……………11分
……………11分
∵二面角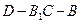 是锐二
是锐二 面角
面角
∴二面角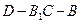 的余弦值为
的余弦值为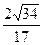 ………………………… 12分
………………………… 12分
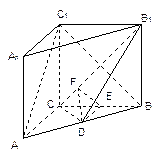
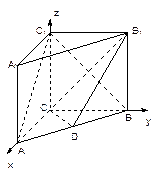
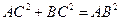
∴ AC⊥BC, …………………2分
又 AC⊥
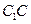 ,且
,且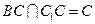
∴ AC⊥平面BCC1,又
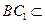 平面BCC1 ……………………………………4分
平面BCC1 ……………………………………4分∴ AC⊥BC1 ………………………………………………………………5分
(Ⅱ)解法一:取
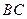 中点
中点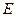 ,过
,过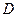 作
作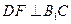 于
于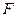 ,连接
,连接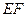 …………6分
…………6分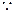
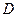 是
是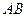 中点,
中点,∴
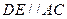 ,又
,又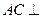 平面
平面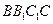
∴
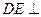 平面
平面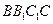 ,
,又
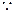
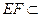 平面
平面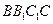 ,
,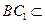 平面
平面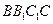
∴
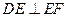
∴
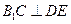 又
又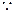
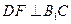 且
且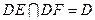
∴
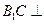 平面
平面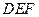 ,
,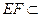 平面
平面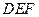 ………8分
………8分∴
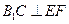 又
又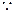
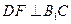
∴
 是二面角
是二面角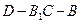 的平面角 ……………………………………10分
的平面角 ……………………………………10分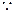 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,∴在
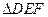 中,
中,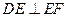 ,
,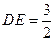 ,
,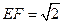
∴
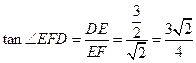 …………………………………………11分
…………………………………………11分∴二面角
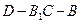 的正切值为
的正切值为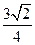 …………………………………………12分
…………………………………………12分解法二:以
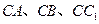 分别为
分别为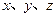 轴建立如图所示空间直角坐标系…………6分
轴建立如图所示空间直角坐标系…………6分 AC=3,BC=4,AA1=4,
AC=3,BC=4,AA1=4,∴
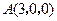 ,
,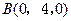
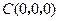 ,
,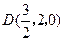 ,
,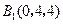 ,
,∴
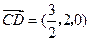 ,
,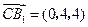
平面
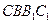 的法向量
的法向量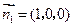 , …………………8分
, …………………8分设平面
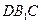 的法向量
的法向量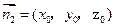 ,
,则
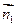 ,
,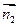 的夹角(或其补角)的大小就是二面角
的夹角(或其补角)的大小就是二面角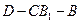 的大小 …………9分
的大小 …………9分则由
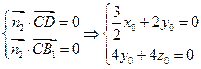 令
令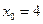 ,则
,则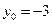 ,
,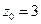 ∴
∴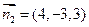 ………………10分
………………10分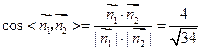 ……………11分
……………11分∵二面角
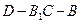 是锐二
是锐二 面角
面角∴二面角
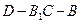 的余弦值为
的余弦值为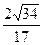 ………………………… 12分
………………………… 12分
练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
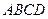 与
与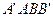 都是边长为
都是边长为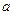 的正方形,点E是
的正方形,点E是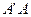 的中点,
的中点,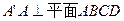
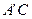
 平面BDE;
平面BDE;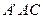 ⊥平面BDE
⊥平面BDE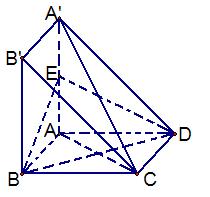
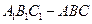 中,
中, 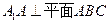 ,
,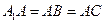 ,
,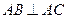 ,点D是
,点D是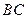 上一点,且
上一点,且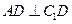 。
。
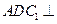 平面
平面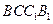 ;
;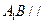 平面
平面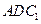 ;
;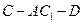 的余弦值
的余弦值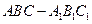 中,侧面
中,侧面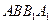 ,
,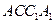 均为正方形,∠
均为正方形,∠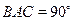 ,点
,点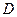 是棱
是棱 的中点.
的中点.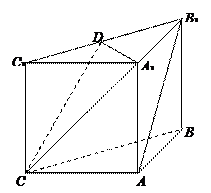
 ⊥平面
⊥平面 ;
;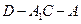 的余弦值.
的余弦值. 中(如图1),
中(如图1),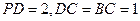 ,
,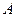 为
为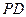 的中点,
的中点,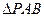 沿
沿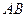 折起,使面
折起,使面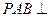 面
面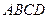 (如图2),点
(如图2),点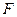 在线段
在线段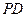 上,
上,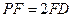 .
.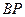 与
与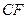 所成角的余弦值;
所成角的余弦值;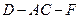 的余弦值;
的余弦值; (3)在四棱锥
(3)在四棱锥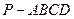 的棱
的棱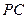 上是否存在一点
上是否存在一点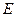 ,使得
,使得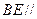 平面
平面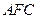 ,若存在,求出
,若存在,求出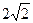 .
.
 中,
中,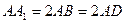 ,且
,且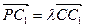
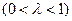 .
.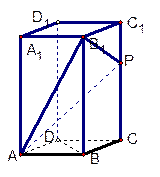
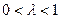 ,总有
,总有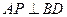 ;
;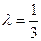 ,求二
,求二 面角
面角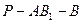 的余弦值;
的余弦值;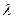 ,使得
,使得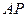 在平面
在平面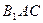 上的射影平分
上的射影平分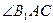 ?若存在,求出
?若存在,求出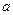 的正方体
的正方体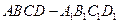 中,
中,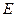 是线段
是线段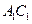 中点,
中点,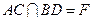 .
.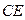 ^
^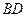 ;(Ⅱ) 求证:
;(Ⅱ) 求证: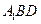 ;
;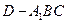 的体积.
的体积.