题目内容
函数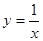 在(0,+∞)上( )
在(0,+∞)上( )
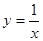 在(0,+∞)上( )
在(0,+∞)上( )| A.既无最大值又无最小值 | B.仅有最小值 |
| C.既有最大值又有最小值 | D.仅有最大值 |
A
试题分析:
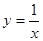 在(0,+∞)上单调递减,所以既无最大值又无最小值.
在(0,+∞)上单调递减,所以既无最大值又无最小值.点评:要求函数的最值,首先应该判断函数的单调性,而要判断函数的单调性,主要是应用定义.

练习册系列答案
相关题目
题目内容
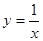 在(0,+∞)上( )
在(0,+∞)上( )| A.既无最大值又无最小值 | B.仅有最小值 |
| C.既有最大值又有最小值 | D.仅有最大值 |
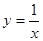 在(0,+∞)上单调递减,所以既无最大值又无最小值.
在(0,+∞)上单调递减,所以既无最大值又无最小值.