题目内容
19. 如图,在四棱锥A-BDEC中,AD⊥平面BDEC,底面BDEC为直角梯形,∠BDE=90°,BC∥DE,AD=DB=$\frac{\sqrt{2}}{2}$,BC=2DE=1,
如图,在四棱锥A-BDEC中,AD⊥平面BDEC,底面BDEC为直角梯形,∠BDE=90°,BC∥DE,AD=DB=$\frac{\sqrt{2}}{2}$,BC=2DE=1,(Ⅰ)求证:面ADC⊥面ABE;
(Ⅱ)求点E到平面ABC的距离.
分析 (1)以D为坐标原点建立空间直角坐标系,根据各边长度求出各点坐标,求出平面ADC和面ABE的法向量,将问题转化为证明两个平面的法向量垂直;
(2)求出平面ABC的法向量,则E到平面ABC的距离为$\overrightarrow{BE}$在平面ABC的法向量上的投影的绝对值.
解答  证明:(1)以D为坐标原点建立如图所示的空间直角坐标系,
证明:(1)以D为坐标原点建立如图所示的空间直角坐标系,
∵AD=DB=$\frac{\sqrt{2}}{2}$,BC=2DE=1,∴A(0,0,$\frac{\sqrt{2}}{2}$),B($\frac{\sqrt{2}}{2}$,0,0),C($\frac{\sqrt{2}}{2}$,1,0),D(0,0,0),E(0,$\frac{1}{2}$,0).
∴$\overrightarrow{DA}$=(0,0,$\frac{\sqrt{2}}{2}$),$\overrightarrow{DC}$=($\frac{\sqrt{2}}{2}$,1,0),$\overrightarrow{BA}$=(-$\frac{\sqrt{2}}{2}$,0,$\frac{\sqrt{2}}{2}$),$\overrightarrow{BE}$=(-$\frac{\sqrt{2}}{2}$,$\frac{1}{2}$,0).
设平面ADC的法向量为$\overrightarrow{{n}_{1}}$=(x,y,z),平面ABE的法向量为$\overrightarrow{{n}_{2}}$=(a,b,c),
则$\overrightarrow{{n}_{1}}⊥\overrightarrow{DA}$,$\overrightarrow{{n}_{1}}⊥\overrightarrow{DC}$,$\overrightarrow{{n}_{2}}⊥\overrightarrow{BA}$,$\overrightarrow{{n}_{2}}⊥\overrightarrow{BE}$.
∴$\left\{\begin{array}{l}{\frac{\sqrt{2}}{2}z=0}\\{\frac{\sqrt{2}}{2}x+y=0}\end{array}\right.$,$\left\{\begin{array}{l}{-\frac{\sqrt{2}}{2}a+\frac{\sqrt{2}}{2}c=0}\\{-\frac{\sqrt{2}}{2}a+\frac{1}{2}b=0}\end{array}\right.$,
令x=$\sqrt{2}$得$\overrightarrow{{n}_{1}}$=($\sqrt{2}$,-1,0),令c=1得$\overrightarrow{{n}_{2}}$=(1,$\sqrt{2}$,1).
∴$\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}$=$\sqrt{2}-\sqrt{2}+0$=0,
∴面ADC⊥面ABE.
(2)$\overrightarrow{BC}$=(0,1,0),
设平面ABC的法向量为$\overrightarrow{{n}_{3}}$=(x,y,z),则$\overrightarrow{{n}_{3}}⊥\overrightarrow{BA}$,$\overrightarrow{{n}_{3}}⊥\overrightarrow{BC}$,
∴$\left\{\begin{array}{l}{-\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}z=0}\\{y=0}\end{array}\right.$,令z=1得$\overrightarrow{{n}_{3}}$=(1,0,1).
∴$\overrightarrow{{n}_{3}}•\overrightarrow{BE}$=-$\frac{\sqrt{2}}{2}$.而|$\overrightarrow{{n}_{3}}$|=$\sqrt{2}$,|$\overrightarrow{BE}$|=$\frac{\sqrt{3}}{2}$,
∴cos<$\overrightarrow{{n}_{3}}$,$\overrightarrow{BE}$>=$\frac{\overrightarrow{{n}_{3}}•\overrightarrow{BE}}{|\overrightarrow{{n}_{3}}||\overrightarrow{BE}|}$=-$\frac{\sqrt{3}}{3}$.
∴E点到平面ABC的距离d=|$\overrightarrow{BE}$|•|cos<$\overrightarrow{{n}_{3}}$,$\overrightarrow{BE}$>|=$\frac{\sqrt{3}}{2}•\frac{\sqrt{3}}{3}$=$\frac{1}{2}$.
点评 本题考查了面面垂直的判定,点到平面的距离,使用空间向量解题是常用方法之一.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | (0,1) | B. | (0,2] | C. | (1,2) | D. | (1,2] |
| A. | 11,25 | B. | 11,27 | C. | 8,27 | D. | 11,8 |
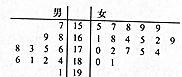 某初中对初二年级的学生进行体质测试,已知初二一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm):
某初中对初二年级的学生进行体质测试,已知初二一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:cm): 如图所示,四棱锥S-ABCD的底面四边形ABCD为平行四边形,其中AC⊥BD,且AC、BD相交于O,∠SBC=∠SBA.
如图所示,四棱锥S-ABCD的底面四边形ABCD为平行四边形,其中AC⊥BD,且AC、BD相交于O,∠SBC=∠SBA.