题目内容
8．设抛物线x2=8y上一点P到x轴的距离是4，则点P到抛物线焦点的距离是（ ）| A． | 12 | B． | 8 | C． | 6 | D． | 4 |
分析 由题意可得点P的纵坐标为4，由抛物线的定义可得点P到该抛物线焦点的距离等于点P到准线y=-2的距离，由此求得结果．
解答 解：由于抛抛物线x2=8y上的一点P到x轴的距离是4，
故点P的纵坐标为4．
再由抛物线x2=8y的准线为y=-2，
结合抛物线的定义可得点P到该抛物线焦点的距离等于点P到准线的距离，
故点P到该抛物线焦点的距离是4-（-2）=6，
故选：C．
点评 本题主要考查抛物线的定义、标准方程，以及简单性质的应用，属于基础题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
19．函数f（x）=tanωx（ω＞0）的图象的相邻两个零点的距离为$\frac{π}{2}$，则$f（\frac{π}{6}）$的值是（ ）
| A． | -$\sqrt{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\sqrt{3}$ | D． | 1 |
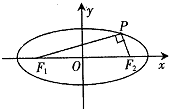如图，P是椭圆$\frac{{x}^{2}}{4}$+y2=1上的一点，F1，F2是椭圆的两个焦点，且∠F1PF2=90°，则|PF1|•|PF2|等于（ ）
某连锁火锅城开业之际，为吸引更多的消费者，开展抽奖活动，前20位顾客可参加如下活动：摇动如图所示的游戏转盘（上面扇形的圆心角都相等），顾客可以免费获得按照指针所指区域的数字10倍金额的店内菜品或饮品，最高120元，每人只能参加一次这个活动．记事件A：获得不多于30元菜品或饮品．