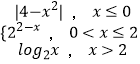Question

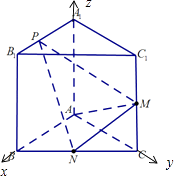
【题目】如图，已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直，AA1=AB=AC=2，BC=2 ，M，N分别是CC1 ， BC的中点，点P在直线A1B1上，且 ．

（1）证明：无论λ取何值，总有AM⊥PN；
（2）当λ取何值时，直线PN与平面ABC所成的角θ最大？并求该角取最大值时的正切值．

Answer 1

【答案】
（1）证明：∵AB=AC=2， ，∴AB2+AC2=BC2，

∴AB⊥AC，即AB、AC、AA1两两相互垂直．

以A为原点建立如图所示的空间直角坐标系A﹣xyz，

则A1（0，0，2），B1（2，0，2），M（0，2，1），N（1，1，0）．

∵ ，∴P（2λ，0，2），∴ =（1﹣2λ，1，﹣2）. ，

∴ ．

∴无论λ取何值，AM⊥PN．

（2）∵ =（0，0，1）是平面ABC的一个法向量．

∴ = ．

∴当λ= 时，θ取得最大值，

此时sinθ= ，cosθ= ，tanθ=2．

【解析】（1）建立空间直角坐标系，求出 ， 的坐标，只需证明 即可；（2）显然平面ABC的法向量为 =（0，0，1），根据sinθ=|cos＜ ， ＞|求出sinθ的最大值，利用同角三角函数的关系求出tanθ．
【考点精析】认真审题，首先需要了解空间中直线与直线之间的位置关系(相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点)，还要掌握空间角的异面直线所成的角(已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则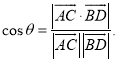)的相关知识才是答题的关键．