题目内容
已知1=12，2+3+4=32，3+4+5+6+7=52，4+5+6+7+8+9+10=72，…，则第n个等式为 ．
考点：归纳推理
专题：计算题,推理和证明
分析：观察所给的等式，等号右边是12，32，52，72…第n个应该是（2n-1）2，左边的式子的项数与右边的底数一致，每一行都是从这一个行数的数字开始相加的，写出结果．
解答：
解：观察下列等式1=12，2+3+4=32，3+4+5+6+7=52，4+5+6+7+8+9+10=72
…
等号右边是12，32，52，72…第n个应该是（2n-1）2
左边的式子的项数与右边的底数一致，
每一行都是从这一个行数的数字开始相加的，
照此规律，第n个等式为n+（n+1）+（n+2）+…+（3n-2）=（2n-1）2．
故答案为：n+（n+1）+（n+2）+…+（3n-2）=（2n-1）2
…
等号右边是12，32，52，72…第n个应该是（2n-1）2
左边的式子的项数与右边的底数一致，
每一行都是从这一个行数的数字开始相加的，
照此规律，第n个等式为n+（n+1）+（n+2）+…+（3n-2）=（2n-1）2．
故答案为：n+（n+1）+（n+2）+…+（3n-2）=（2n-1）2
点评：本题考查归纳推理，考查对于所给的式子的理解，主要看清楚式子中的项与项的数目与式子的个数之间的关系，本题是一个易错题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
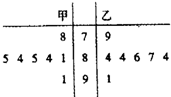为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛，其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示．