题目内容
11.在△ABC中,设边a,b,c所对的角分别为A,B,C,A,B,C都不是直角,且accosB+bccosA=a2-b2+8cosA(Ⅰ)若sinB=2sinC,求b,c的值;
(Ⅱ)若$a=\sqrt{6}$,求△ABC面积的最大值.
分析 (Ⅰ)由已知利用余弦定理化简可得2bccosA=8cosA,由于cosA≠0,可求bc=4,由正弦定理化简已知可得b=2c,联立可求b,c的值.
(Ⅱ)由余弦定理,基本不等式可求$cosA≥\frac{1}{4}$,进而可求$sinA≤\frac{{\sqrt{15}}}{4}$,利用三角形面积公式即可解得得解其最大值.
解答 (本题满分为12分)
解:(Ⅰ)∵$ac\frac{{{a^2}+{c^2}-{b^2}}}{2ac}+bc\frac{{{b^2}+{c^2}-{a^2}}}{2bc}={a^2}-{b^2}+8cosA$,
∴b2+c2-a2=8cosA,--------(2分)
∴2bccosA=8cosA,
∵cosA≠0,
∴bc=4,------(4分)
由正弦定理得:b=2c,
∴$b=2\sqrt{2},c=\sqrt{2}$.------(6分)
(Ⅱ)a2=b2+c2-2bccosA≥2bc-2bccosA,
即6≥8-8cosA,
∴$cosA≥\frac{1}{4}$,当且仅当b=c时取等号,----------(10分)
∴$sinA≤\frac{{\sqrt{15}}}{4}$,
∴$S=\frac{1}{2}bcsinA≤\frac{{\sqrt{15}}}{2}$,
∴$S=\frac{1}{2}bcsinA≤\frac{{\sqrt{15}}}{2}$,
所以面积最大值为$\frac{{\sqrt{15}}}{2}$------(12分)
点评 本题主要考查了余弦定理,正弦定理,基本不等式,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
2.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,若对任意给定的y∈(2,+∞),都存在唯一的x∈R,满足f(f(x))=2a2y2+ay,则正实数a的最小值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
19.设Sn为等比数列{an}的前n项和,a3=8a6,则$\frac{S_4}{S_2}$的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | 5 |
6.设函数f(x)是R上的奇函数,f(x+π)=-f(x),当0≤x≤$\frac{π}{2}$时,f(x)=cosx-1,则-2π≤x≤2π时,f(x)的图象与x轴所围成图形的面积为( )
| A. | 4π-8 | B. | 2π-4 | C. | π-2 | D. | 3π-6 |
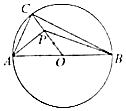 如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )
如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )