题目内容
 直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.(1)求证:AC⊥平面BB1C1C;
(2)若P为A1B1的中点,求证:DP∥平面ACB1.
分析:(1)直棱柱ABCD-A1B1C1D1中,由BB1⊥平面ABCD,知BB1⊥AC,有∠BAD=∠ADC=90°,知AB=2AD=2CD=2,由此能够证明AC⊥平面BB1C1C.
(2)由P为A1B1的中点,知PB1∥AB,且PB1=
AB,由此能够证明DP∥面ACB1.
(2)由P为A1B1的中点,知PB1∥AB,且PB1=
| 1 |
| 2 |
解答:证明:(1)直棱柱ABCD-A1B1C1D1中,
BB1⊥平面ABCD,
∴BB1⊥AC,
∵∠BAD=∠ADC=90°,
AB=2AD=2CD=2,
∴AC=
,∴BC=
,∴BC⊥AC,
∴AC⊥平面BB1C1C.
(2)由P为A1B1的中点,知PB1∥AB,
且PB1=
AB,
∵DC∥AB,DC=
AB,
∴DC∥PB1,且DC=PB1,
∴DCB1P为平行四边形,从而CB1∥DP,
∵CB1?面ACB1,DP?面ACB1,
∴DP∥面ACB1.
BB1⊥平面ABCD,
∴BB1⊥AC,
∵∠BAD=∠ADC=90°,
AB=2AD=2CD=2,
∴AC=
| 2 |
| 2 |
∴AC⊥平面BB1C1C.
(2)由P为A1B1的中点,知PB1∥AB,
且PB1=
| 1 |
| 2 |
∵DC∥AB,DC=
| 1 |
| 2 |
∴DC∥PB1,且DC=PB1,
∴DCB1P为平行四边形,从而CB1∥DP,
∵CB1?面ACB1,DP?面ACB1,
∴DP∥面ACB1.
点评:本题考查直线与平面垂直的证明和直线与平面平行的证明,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
相关题目
 16、如图,底面为菱形的直四棱柱ABCD-A1B1C1D1中,E、F分别为A1B1、B1C1的
16、如图,底面为菱形的直四棱柱ABCD-A1B1C1D1中,E、F分别为A1B1、B1C1的 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2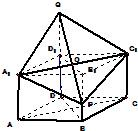 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形,Q是侧棱DD1(DD1>
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形,Q是侧棱DD1(DD1> 在直四棱柱ABCD-A1B1C1D1中,AA1=3,AD=DC=2,AB=1,AD⊥DC,AB∥CD.
在直四棱柱ABCD-A1B1C1D1中,AA1=3,AD=DC=2,AB=1,AD⊥DC,AB∥CD.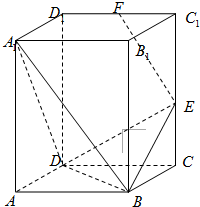 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是∠DAB=60°的菱形,AA1=4,AB=2,点E在棱CC1上,点F是棱C1D1的中点;
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是∠DAB=60°的菱形,AA1=4,AB=2,点E在棱CC1上,点F是棱C1D1的中点;