题目内容
 在直四棱柱ABCD-A1B1C1D1中,AA1=3,AD=DC=2,AB=1,AD⊥DC,AB∥CD.
在直四棱柱ABCD-A1B1C1D1中,AA1=3,AD=DC=2,AB=1,AD⊥DC,AB∥CD.(1)设E为DC的中点,求证:D1E∥平面A1BD;
(2)求二面角A1-BD-C1的余弦值.
分析:(1)利用直四棱柱平行四边形的性质、线面平行的判定定理即可得出;
(2)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得出二面角的平面角.
(2)通过建立空间直角坐标系,利用两个平面的法向量的夹角即可得出二面角的平面角.
解答:(1)证明:如图所示, 连接BE.
连接BE.
∵E为DC的中点,∴DE=
DC=1.
∵AB=1,∴DE=AB.
又∵AB∥DE,∴四边形ABED是平行四边形,∴BE
AD.
由直四棱柱ABCD-A1B1C1D1,可得AD
A1D1.
∴A1D1
BE.
∴四边形BED1A1是平行四边形.
∴D1E∥A1B.
又D1E?平面A1BD,A1B?平面A1BD,
∴D1E∥平面A1BD;
(2)解:如图所示,建立空间直角坐标系,则D(0,0,0),B(2,1,0),A1(2,0,3),C1(0,2,3).
∴
=(2,0,3),
=(2,1,0),
=(0,2,3).
设平面A1BD的法向量为
=(x,y,z),则
,令z=2,则x=-3,y=6.
∴
=(-3,6,2).
设平面DBC1的法向量为
,同理可得
=(3,-6,4).
∴cos<
,
>=
=
=-
.
∴二面角A1-BD-C1的余弦值为
.
 连接BE.
连接BE.∵E为DC的中点,∴DE=
| 1 |
| 2 |
∵AB=1,∴DE=AB.
又∵AB∥DE,∴四边形ABED是平行四边形,∴BE
| ∥ |
. |
由直四棱柱ABCD-A1B1C1D1,可得AD
| ∥ |
. |
∴A1D1
| ∥ |
. |
∴四边形BED1A1是平行四边形.
∴D1E∥A1B.
又D1E?平面A1BD,A1B?平面A1BD,
∴D1E∥平面A1BD;
(2)解:如图所示,建立空间直角坐标系,则D(0,0,0),B(2,1,0),A1(2,0,3),C1(0,2,3).
∴
| DA1 |
| DB |
| DC1 |
设平面A1BD的法向量为
| n |
|
∴
| n |
设平面DBC1的法向量为
| m |
| m |
∴cos<
| n |
| m |
| ||||
|
|
| -9-36+8 | ||||
|
37
| ||
| 427 |
∴二面角A1-BD-C1的余弦值为
37
| ||
| 427 |
点评:熟练掌握直四棱柱平行四边形的性质、线面平行的判定定理、通过建立空间直角坐标系利用两个平面的法向量的夹角得出二面角的平面角等是解题的关键.

练习册系列答案
相关题目
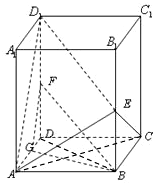 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.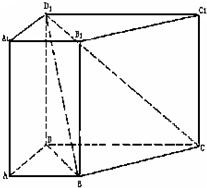 在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.
在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.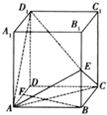 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE= 在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.
在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.