题目内容
19.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{y≥0}\\{kx+y-3k≤0}\end{array}\right.$且目标函数z=y-x的最大值是4,则k等于$\frac{3}{4}$.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{y≥0}\\{kx+y-3k≤0}\end{array}\right.$作出可行域如图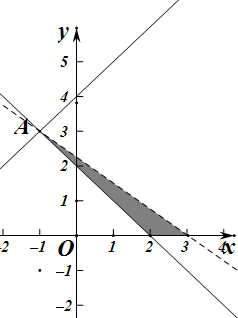 ,因为直线kx+y-3k=0过定点(3,0),所以只有目标函数z=y-x过A时取最大值是4,
,因为直线kx+y-3k=0过定点(3,0),所以只有目标函数z=y-x过A时取最大值是4,
由$\left\{\begin{array}{l}{x+y-2=0}\\{y-x=4}\end{array}\right.$,解得A(-1,3)此时,-k=$\frac{3-0}{-1-3}$=-$\frac{3}{4}$,所以k=$\frac{3}{4}$;
故答案为:$\frac{3}{4}$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.如果约束条件中含有参数,我们可以先画出不含参数的几个不等式对应的平面区域,分析取得最优解是哪两条直线的交点,然后得到一个含有参数的方程(组),代入另一条直线方程,消去x,y后,即可求出参数的值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.已知函数f(x)=ax2-4ax-lnx,则f(x)在(1,3)上不单调的一个充分不必要条件是( )
| A. | a∈(-∞,$\frac{1}{6}$) | B. | a∈(-$\frac{1}{2}$,+∞) | C. | a∈(-$\frac{1}{2}$,$\frac{1}{6}$) | D. | a∈($\frac{1}{2}$,+∞) |
10.设曲线y=$\frac{x+1}{x-1}$在点(2,3)处的切线与直线ax+y+1=0平行,则a=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | 2 |
14.已知函数$f(x)=sin({wx+ϕ}),({w>0,|ϕ|<\frac{π}{2}})$,其相邻两个最高点之间的距离是π,且函数$f({x+\frac{π}{12}})$是偶函数,下列判断正确的是( )
| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)在$[{\frac{3π}{4},π}]$上单调递增 | |
| C. | 函数f(x)的图象关于直线$x=-\frac{7π}{12}$对称 | |
| D. | 函数f(x)的图象关于点$({\frac{π}{12},0})$对称- |
11.若函数f(x)的定义域是[0,1],则函数f(2x)+f(x+$\frac{1}{3}$)的定义域为( )
| A. | [-$\frac{1}{3}$,$\frac{2}{3}$] | B. | [-$\frac{1}{3}$,$\frac{1}{2}$] | C. | [0,$\frac{1}{2}$] | D. | [0,$\frac{1}{3}$] |
 如图所示,l1,l2是互相垂直的异面直线,MN是它们的公垂线段,点A,B在直线l1上,且位于M点的两侧,C在l2上,AM=BM=NM=CN
如图所示,l1,l2是互相垂直的异面直线,MN是它们的公垂线段,点A,B在直线l1上,且位于M点的两侧,C在l2上,AM=BM=NM=CN