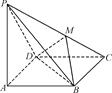
题目内容
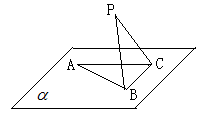
如图,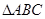 在平面
在平面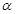 内,
内, ,
,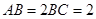 ,P为平面
,P为平面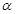 外一个动点,且PC=
外一个动点,且PC=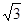 ,
,
(1)问当PA的长为多少时,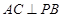
(2)当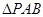 的面积取得最大值时,求直线BC与平面PAB所成角的大小
的面积取得最大值时,求直线BC与平面PAB所成角的大小
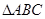 在平面
在平面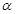 内,
内, ,
,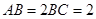 ,P为平面
,P为平面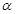 外一个动点,且PC=
外一个动点,且PC=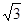 ,
,

(1)问当PA的长为多少时,
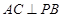
(2)当
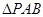 的面积取得最大值时,求直线BC与平面PAB所成角的大小
的面积取得最大值时,求直线BC与平面PAB所成角的大小(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)由分析可知当
 时,
时,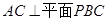 ,则
,则 ,由勾股定理可求得
,由勾股定理可求得 。(2)因为
。(2)因为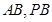 为定值,且
为定值,且 ,
,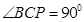 ,所以当
,所以当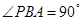 时,
时,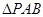 的面积取得最大值。分析可知
的面积取得最大值。分析可知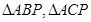 均是以
均是以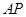 为底的等腰三角形,故取
为底的等腰三角形,故取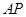 中点
中点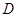 ,连接
,连接 。则有
。则有 ,从而可得
,从而可得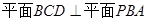 ,可知
,可知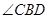 就是直线
就是直线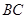 与平面PAB所成角,在
与平面PAB所成角,在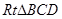 中可求此角。
中可求此角。试题解析:(1)因为
 ,所以
,所以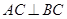 ,当
,当 时,
时,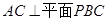 ,而
,而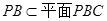 ,所以
,所以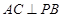 ,此时,
,此时,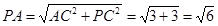 ,即当PA=
,即当PA= 时,
时,
(2)
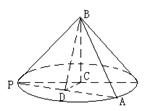
在
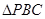 中,因为PC=
中,因为PC=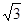 ,
, ,
,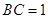 ,所以
,所以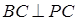 ,当
,当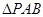 的面积取得最大值时,
的面积取得最大值时,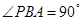 ,(如图)在
,(如图)在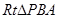 中,因为
中,因为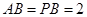 ,取
,取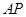 中点
中点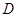 ,连接
,连接 。则
。则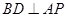 ,因为
,因为 且点
且点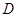 为
为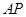 中点,所以
中点,所以 ,因为
,因为 ,所以
,所以 ,由此可求得
,由此可求得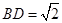 ,又在
,又在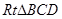 中,
中,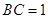 ,所以
,所以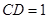 ,由于
,由于 ,所以
,所以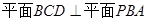 ,所以
,所以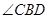 就是直线
就是直线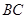 与平面PAB所成角,在
与平面PAB所成角,在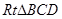 中,因为
中,因为 ,所以
,所以 ,所以直线BC与平面
,所以直线BC与平面 所成角的大小为
所成角的大小为

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
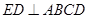 ,ED=1,
,ED=1,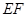 //BD,且
//BD,且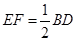 .
.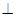 平面BDEF;
平面BDEF;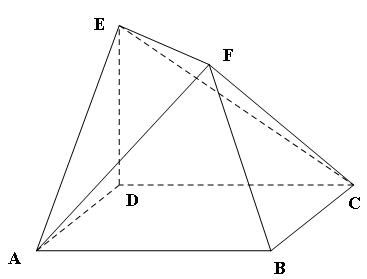
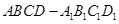
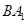 异面
异面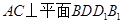

 分别是正方体
分别是正方体 的棱
的棱 的中点,点
的中点,点 分别是线段
分别是线段 与
与 上的点,则与平面
上的点,则与平面 垂直的直线
垂直的直线 有( )
有( )
 外一点可以作无数条直线与平面
外一点可以作无数条直线与平面 垂直平面
垂直平面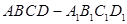 中,线段
中,线段 上(不包括端点)各有一点
上(不包括端点)各有一点 ,且
,且 ,下列说法中,不正确的是( )
,下列说法中,不正确的是( ) 四点共面
四点共面 与平面
与平面 所成的角为定值
所成的角为定值
 的大小为
的大小为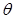 ,则
,则 的最小值为
的最小值为
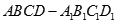 中,
中,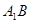 与平面
与平面 所成的角的大小是
所成的角的大小是