题目内容
函数f（x）=6cos2| ωx |
| 2 |
| 3 |
（1）若x∈[0，1]，求函数f（x）的值域；
（2）若f（x0）=
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
| πx0 |
| 4 |
| π |
| 3 |
考点：两角和与差的余弦函数,二倍角的余弦,由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的求值,三角函数的图像与性质
分析：（1）化简可得f（x）=2
sin（ωx+
），由已知可得周期，进而可得ω，可得函数的解析式，由x的范围可得；（2）由题意可得sin（
x0+
）=
，由同角三角函数的基本关系可得要求的值．
| 3 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| 4 |
| 5 |
解答：
解：（1）由已知得f（x）=6cos2
+
sinωx-3
=3cosωx+
sinωx=2
sin（ωx+
）
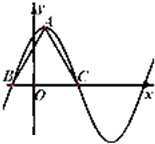
又△ABC为正三角形，且高为2
，可得BC=4．
∴函数f（x）的最小正周期为8，即
=8，
解得ω=
，∴f（x）=2
sin（
x+
），
∵x∈[0，1]，∴
x+
∈[
，
]，
∴sin（
x+
）∈[
，1]
∴f（x）∈[3，2
]，
∴函数f（x）的值域为：[3，2
]；
（2）∵f（x0）=
，
∴f（x0）=2
sin（
x0+
）=
，
化简可得sin（
x0+
）=
，
∵x0∈（-
，
），∴（
x0+
）∈（-
，
）
∴cos（
+
）=
=
| ωx |
| 2 |
| 3 |
=3cosωx+
| 3 |
| 3 |
| π |
| 3 |
又△ABC为正三角形，且高为2
| 3 |
∴函数f（x）的最小正周期为8，即
| 2π |
| ω |
解得ω=
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 3 |
∵x∈[0，1]，∴
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 7π |
| 12 |
∴sin（
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
∴f（x）∈[3，2
| 3 |
∴函数f（x）的值域为：[3，2
| 3 |
（2）∵f（x0）=
8
| ||
| 5 |
∴f（x0）=2
| 3 |
| π |
| 4 |
| π |
| 3 |
8
| ||
| 5 |
化简可得sin（
| π |
| 4 |
| π |
| 3 |
| 4 |
| 5 |
∵x0∈（-
| 10 |
| 3 |
| 2 |
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
∴cos（
| πx0 |
| 4 |
| π |
| 3 |
1-sin2(
|
| 3 |
| 5 |
点评：本题考查两角和与差的三角函数公式，涉及同角三角函数的基本关系和三角函数的值域，属中档题．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
函数f（x）=cosπx-|log2|x-1||的所有零点之和为（ ）
| A、6 | B、4 | C、2 | D、0 |
已知函数f（x）的导数f′（x）=（x+2）（x-a），若f（x）在x=a处取得极大值，则函数f（x）的单调减区间为（ ）
| A、[a，-2] |
| B、[a，+∞） |
| C、（-∞，-2] |
| D、[-2，a] |
设[x]表示不超过x的最大整数，如[1.5]=1，[-1.5]=-2，若函数f（x）=
，则函数g（x）=[f（x）]+[f（-x）]的值域为（ ）
| 1-ex |
| 1+ex |
| A、{-1} |
| B、{-1，0，1} |
| C、{0} |
| D、{-1，0} |