题目内容
如图,在四棱锥P﹣ABCD中,侧棱PA丄底面ABCD底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE.
⑴若F为PE的中点,求证BF∥平面ACE;
⑵求三棱锥P﹣ACE的体积.

解:(1)若F为PE的中点,由于底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE,故E、F都是线段PD的三等分点.
设AC与BD的交点为O,则OE是△BDF的中位线,
故有BF∥OE,而OE在平面ACE内,BF不在平面ACE内,故BF∥平面ACE.
(2)由于侧棱PA丄底面ABCD,且ABCD为矩形,
故有CD⊥PA,CD⊥AD,故CD⊥平面PAE,.
三棱锥P﹣ACE的体积VP﹣ACE=VC﹣PAE
= S△PAE•CD=
S△PAE•CD= •(
•( •S△PAD)•AB=
•S△PAD)•AB= (
( •
• •PA•PD)•AB=
•PA•PD)•AB= •PA•PD•AB=
•PA•PD•AB= •1•2•1=
•1•2•1= .
.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
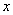 的二项式
的二项式 展开式中的常数项是
展开式中的常数项是  、
、 、
、 的大小关系为( )
的大小关系为( ) B.
B.
 D.
D.

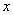 的方程
的方程 在区间
在区间 上有解,则实数
上有解,则实数 的取值范围是
的取值范围是 ,在矩阵M
,在矩阵M 对应的变换作用下得到曲线
对应的变换作用下得到曲线 ,
, 对应的变换作用下得到曲线
对应的变换作用下得到曲线 ,求曲线
,求曲线 的值为 .
的值为 . 
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E: +
+ =1.
=1. 在
在 处的切线方程为 。
处的切线方程为 。