题目内容
【题目】已知函数
，且曲线
与直线
相切于点
，
（1）求
；
（2）若
，求实数
的取值范围.
【答案】(1) 
；(2) 
【解析】
（1）先由题意得到
，求出
，再对函数求导，根据
求出
，从而可得到解析式；
（2）先令
，先由题意确定
，再由函数奇偶性的概念，易得到
为偶函数，因此只需
时，
；对函数求导，分别讨论，
两种情况，用导数的方法研究其单调性，最值等，即可得出结果.
（1）由题意可得：，解得
，
由
得
．
所以．
（2）令 ，
由得
，所以．
显然为偶函数，所以只需时，．
，
当时，
，即在
上单调递增，
所以
，
从而时，
成立．
当时，因为
在
上单调递增，
又
时，
；
时，
，
所以存在
，使得
，
因此
时，
，
，即在
上单调递减，
所以时，
，与矛盾，
因此时不成立．
综上，满足题设的
的取值范围是
阅读快车系列答案【题目】某市春节期间7家超市的广告费支出
（万元）和销售额
（万元）数据如下：
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
参数数据及公式：
，
，
，
，
，
，
.
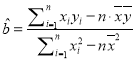（1）若用线性回归模型拟合y与x的关系，求y关于x的线性回归方程；
（2）用对数回归模型拟合y与x的关系，可得回归方程：
，经计算得出线性回归模型和对数模型的
分别约为0.75和0.97，请用说明选择哪个回归模型更合适，并用此模型预测A超市广告费支出为8万元时的销售额.
【题目】为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：kg），并将所得数据分组，画出频率分布直方图（如图所示）．
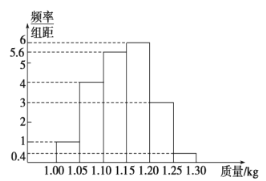
（1）在下面表格中填写相应的频率；
分组 | 频率 |
| |
| |
| |
| |
| |
|
（2）估计数据落在
中的概率；
（3）将上面捕捞的100条鱼分别作一记分组频率号后再放回水库．几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条．请根据这一情况来估计该水库中鱼的总条数．
