题目内容
已知椭圆方程
+y2=1,不过原点的直线l与椭圆交于P、Q两点,且直线OP、PQ、OQ的斜率成等比数列,求S△OPQ的取值范围.
| x2 |
| 4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设P(x1,y1),Q(x2,y2).由题意可设直线l的方程为:y=kx+t(t≠0).与椭圆的方程联立可得(1+4k2)x2+8ktx+4t2-4=0.由△>0,可得1+4k2>t2.得到根与系数的关系.利用直线OP、PQ、OQ的斜率成等比数列,可得
•
=k2,化为4k2=1.同时得到t2<2.利用弦长公式可得|PQ|=
=2
,利用点到直线的距离公式可得:原点O到直线PQ的距离d=
.利用S△OPQ=
|PQ|d=
,再利用基本不等式即可得出.
| y1 |
| x1 |
| y2 |
| x2 |
| (1+k2)[(x1+x2)2-4x1x2] |
| (1+k2)(2-t2) |
| |t| | ||
|
| 1 |
| 2 |
| (2-t2)t2 |
解答:
解:设P(x1,y1),Q(x2,y2).
由题意可设直线l的方程为:y=kx+t(t≠0,±1).
联立
,
化为(1+4k2)x2+8ktx+4t2-4=0.
△=64k2t2-4(4t2-4)(1+4k2)>0,化为1+4k2>t2.
∴x1+x2=-
,x1x2=
.
∵直线OP、PQ、OQ的斜率成等比数列,
∴
•
=k2,
∴(kx1+t)(kx2+t)=k2x1x2,
化为tk(x1+x2)+t2=0,
∴
+t=0,
∴4k2=1.
∴t2<2.
∴|PQ|=
=
=2
,
原点O到直线PQ的距离d=
.
∴S△OPQ=
|PQ|d=
≤
=1,由于t2≠1,因此不取等号.
∴S△OPQ的取值范围是(0,1).
由题意可设直线l的方程为:y=kx+t(t≠0,±1).
联立
|
化为(1+4k2)x2+8ktx+4t2-4=0.
△=64k2t2-4(4t2-4)(1+4k2)>0,化为1+4k2>t2.
∴x1+x2=-
| 8kt |
| 1+4k2 |
| 4t2-4 |
| 1+4k2 |
∵直线OP、PQ、OQ的斜率成等比数列,
∴
| y1 |
| x1 |
| y2 |
| x2 |
∴(kx1+t)(kx2+t)=k2x1x2,
化为tk(x1+x2)+t2=0,
∴
| -8k2t |
| 1+4k2 |
∴4k2=1.
∴t2<2.
∴|PQ|=
| (1+k2)[(x1+x2)2-4x1x2] |
(1+k2)[(
|
| (1+k2)(2-t2) |
原点O到直线PQ的距离d=
| |t| | ||
|
∴S△OPQ=
| 1 |
| 2 |
| (2-t2)t2 |
(
|
∴S△OPQ的取值范围是(0,1).
点评:本题考查了直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式、基本不等式的性质、等比数列的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、48-16π |
| B、96-4π |
| C、96-8π |
| D、48-4π |
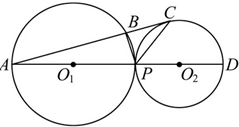 如图,⊙O1和⊙O2外切于点P,延长PO1交⊙O1于点A,延长PO2交⊙O2于点D,若AC与⊙O2相切于点C,且交⊙O1于点B.求证:
如图,⊙O1和⊙O2外切于点P,延长PO1交⊙O1于点A,延长PO2交⊙O2于点D,若AC与⊙O2相切于点C,且交⊙O1于点B.求证: