题目内容
讨论解关于x的方程lgx+lg(4-x)=lg(a+2x)的解的个数.
考点:对数的运算性质
专题:函数的性质及应用
分析:由函数的定义域,得0<x<4,a+2x>0,从而x2-2x+a=0,由此利用分类讨论思想推导出当a=1时,方程只有一个根,x=1;当0<a<1时,方程有两个根,分别是x1=1+
,x2=1-
;当-8<a≤0时,方程有一个根,是x1=1+
;当a>1或a≤-8时,方程无解.
| 1-a |
| 1-a |
| 1-a |
解答:
解:首先根据函数的定义域,得
,
∴0<x<4,a+2x>0…(1)
在上述条件下,原方程可改写为,
x(4-x)=a+2x,
整理,得:x2-2x+a=0…(2)
由△=4-4a=4(1-a)≥0,得a≤1…(3)
当a=1时,只有一个根,x=1,满足条件(1)要求,故是原方程的根.
当a<1时,方程(2)两个根分别为:x1=1+
,x2=1-
,
对于x1:0<1+
<4…(5),a+2(1+
)>0…(6)
解方程(5),得
<3,解得a>-8,
解方程(6),得a+2(1+
)>0,解得a>-8,
即对x1,仅当-8<a<1 时是原方程的根.
对于x2:0<1-
<4…(7),a+2(1-
)>0…(8)
解方程(7),得0<a<1,
解方程(8),得
<
+1,
当a<-2时,不可能成立.当a≥-2时,a(a+8)>0,解得a>0,
即对x2,仅当0<a<1时是原方程的根.
综上:当a=1时,方程只有一个根,x=1;
当0<a<1时,方程有两个根,分别是x1=1+
,x2=1-
;
当-8<a≤0时,方程有一个根,是x1=1+
;
当a>1或a≤-8时,方程无解.
|
∴0<x<4,a+2x>0…(1)
在上述条件下,原方程可改写为,
x(4-x)=a+2x,
整理,得:x2-2x+a=0…(2)
由△=4-4a=4(1-a)≥0,得a≤1…(3)
当a=1时,只有一个根,x=1,满足条件(1)要求,故是原方程的根.
当a<1时,方程(2)两个根分别为:x1=1+
| 1-a |
| 1-a |
对于x1:0<1+
| 1-a |
| 1-a |
解方程(5),得
| 1-a |
解方程(6),得a+2(1+
| 1-a |
即对x1,仅当-8<a<1 时是原方程的根.
对于x2:0<1-
| 1-a |
| 1-a |
解方程(7),得0<a<1,
解方程(8),得
| 1-a |
| a |
| 2 |
当a<-2时,不可能成立.当a≥-2时,a(a+8)>0,解得a>0,
即对x2,仅当0<a<1时是原方程的根.
综上:当a=1时,方程只有一个根,x=1;
当0<a<1时,方程有两个根,分别是x1=1+
| 1-a |
| 1-a |
当-8<a≤0时,方程有一个根,是x1=1+
| 1-a |
当a>1或a≤-8时,方程无解.
点评:本题考查方程的解的个数的讨论,是中档题,解题时要认真审题,注意对数运算性质和分类讨论思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)=cos30°,则 f′(x)的值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
函数f(x)=
,则f[f(
)]的值是( )
|
| 1 |
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
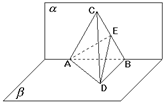 已知平面α⊥平面β,交线为AB,C∈α,D∈β,AB=AC=BC=4
已知平面α⊥平面β,交线为AB,C∈α,D∈β,AB=AC=BC=4