题目内容
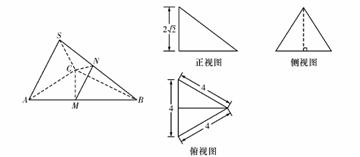
下图分别为三棱锥S-ABC的直观图与三视图,在直观图中SA=SC,M,N分别为AB,SB的中点.
(Ⅰ)求证:AC⊥SB;
(Ⅱ)求二面角M-NC-B的余弦值。
(Ⅰ)求证:AC⊥SB;
(Ⅱ)求二面角M-NC-B的余弦值。
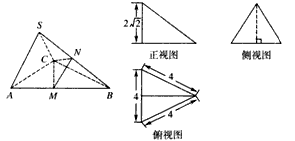
解:由题意知,SA=SC=2 ,侧面SAC⊥底面ABC, ,侧面SAC⊥底面ABC, 底面△ABC为正三角形, (Ⅰ)取AC的中点O,连接OS,OB, 因为SA=SC,AB=BC, 所以AC⊥SO,AC⊥OB, 所以AC⊥平面OSB, 所以AC⊥SB. (Ⅱ)如图所示建立空间直角坐标系O-xyz, 则  , , , ,∴  , , , ,设n=(x,y,z)为平面CMN的一个法向量, 则  ,取z=1,则 ,取z=1,则 , ,所以,  , ,又由(Ⅰ)得,  , ,设m=(a,b,c)为平面NBC的法向量, 由  得 得 , ,令c=1,则  , ,所以,  , ,所以,二面角M-NC-B的余弦值为  。 。 |
 |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

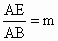 ,
,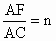 ,则
,则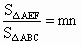 .拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若
.拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若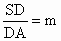 ,
,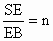 ,
,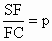 ,则
,则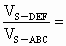 ________.
________.
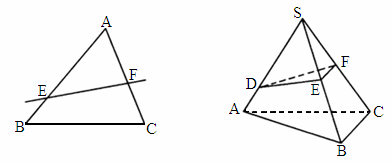
 (1)求证:
(1)求证: