题目内容
9.双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的焦点到渐近线的距离为4.分析 根据题意,先由题中条件求出焦点坐标和渐近线方程,再代入点到直线的距离公式即可求出结论.
解答 解:根据题意,双曲线的方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1,其中a=3,b=4;
其焦点坐标为(-5,0),(5,0),渐近线方程为y=±$\frac{4}{3}$x,即4x±3y=0,
则焦点到其渐近线的距离d=$\frac{|20|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{20}{5}$=4;
故答案为:4.
点评 本题考查双曲线的简单集合性质,关键是正确求出该双曲线的焦点以及渐进线方程.

练习册系列答案
相关题目
19.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F1作圆x2+y2=a2的切线,并延长交双曲线右支于点P,过右焦点F2作圆的切线交F1P于M,且M为F1P的中点,则双曲线的离心率e∈( )
| A. | (1,$\sqrt{2}$) | B. | ($\sqrt{2}$,$\sqrt{3}$) | C. | ($\sqrt{3},2$) | D. | (2,$\sqrt{5}$) |
20.已知函数f(x)=x3-3ax,若f(x)存在唯一的零点x0,则实数a的取值范围是( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-∞,0] |
17.i是虚数单位,设复数z1=1+2i,z2=-3i,则z1•z1=( )
| A. | -6-3i | B. | 2-i | C. | 6-3i | D. | 6+3i |
4.如果f(x)是定义在R上的奇函数,那么下列函数中,一定为偶函数的是( )
| A. | y=x+f(x) | B. | y=xf(x) | C. | y=x2+f(x) | D. | y=x2f(x) |
19.已知点O为坐标原点,点M在双曲线C:x2-y2=λ(λ为正常数)上,过点M作双曲线C的某一条渐近线的垂线,垂足为N,则|ON|•|MN|的值为( )
| A. | $\frac{λ}{4}$ | B. | $\frac{λ}{2}$ | C. | λ | D. | 无法确定 |
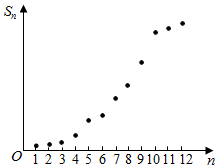 某市2015年前n个月空气质量优良的总天数Sn与n之间的关系如图所示.若前m月的月平均空气质量优良天数最大,则m值为( )
某市2015年前n个月空气质量优良的总天数Sn与n之间的关系如图所示.若前m月的月平均空气质量优良天数最大,则m值为( )